作者與來源
Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang and P. S. Yu, "A Comprehensive Survey on Graph Neural Networks," in IEEE Transactions on Neural Networks and Learning Systems, vol. 32, no. 1, pp. 4-24, Jan. 2021, doi: 10.1109/TNNLS.2020.2978386.
四點貢獻
- New Taxonomy: GNNs are categorized into four groups: recurrent GNNs(RecGNN), convolutional GNNs(ConvGNNs), graph autoencoders(GAEs), and spatial-temporal GNNs(STGNNs)
- Comprehensive Review: For each type of GNNs, we provide detailed descriptions of representative models, make the necessary comparison and summary the corresponding algorithms.
- Abundant Resources: We collect abundant resources on GNNs, including state-of-the-art models, benchmark data sets, open-source codes, and practical applications.
- Future Directions
Notation

GNN分類
Recurrent Graph Neural Networks: These are mostly pioneer works of GNNs. RecGNNs aim to learn node representations with recurrent neural architectures. They assume a node in a graph constantly exchanges information/message with its neighbors until a stable equilibrium is reached.
Convolutional Graph Neural Networks: These generalize the operation of convolution from grid data to graph data. The main idea is to generate a node
’s representation by aggregating its own features and neighbors’ features , where . Different from RecGNNs, ConvGNNs stack multiple graph convolutional layers to extract high-level node representations. Graph Autoencoders: These are unsupervised learning frameworks that encode nodes/graphs into a latent vector space and reconstruct graph data from the encoded information. GAEs are used to learn network embeddings and graph generative distributions. For network embedding, GAEs learn latent node representations through reconstructing graph structural information, such as the graph adjacency matrix. For graph generation, some methods generate nodes and edges of a graph step by step, while other methods output a graph all at once.
Spatial–Temporal Graph Neural Networks: These aim to learn hidden patterns from spatial–temporal graphs. The key idea of STGNNs is to consider spatial dependence and temporal dependence at the same time. Many current approaches integrate graph convolutions to capture spatial dependence with RNNs or CNNs to model temporal dependence.
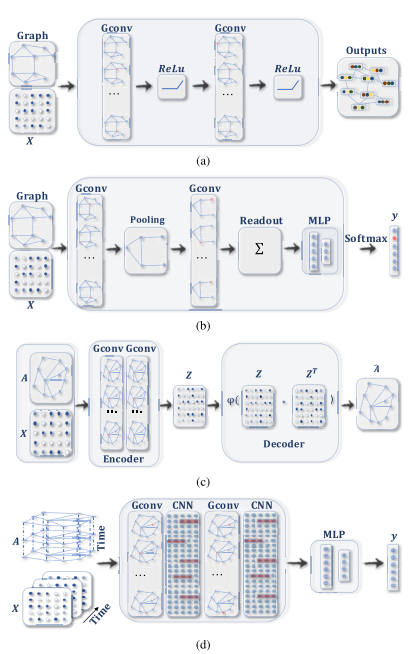
(a):ConvGNN with multiple graph convolutional layers
(b):ConvGNN with pooling and readout layers for graph classification
(c):GAE for network embedding
(d):STGNN for spatial–temporal graph forecasting
三種典型應用
Semisupervised Learning for Node-Level Classification: Given a single network with partial nodes being labeled and others remaining unlabeled, ConvGNNs can learn a robust model that effectively identifies the class labels for the unlabeled nodes. 對於部分有標籤的node,可以用ConvGNN進行節點分類。
Supervised Learning for Graph-Level Classification:Graph-level classification aims to predict the class label(s) for an entire graph.
Unsupervised Learning for Graph Embedding: When no class labels are available in graphs, we can learn the graph embedding in a purely unsupervised way in an end-to-end framework.
不同GNN模型比較
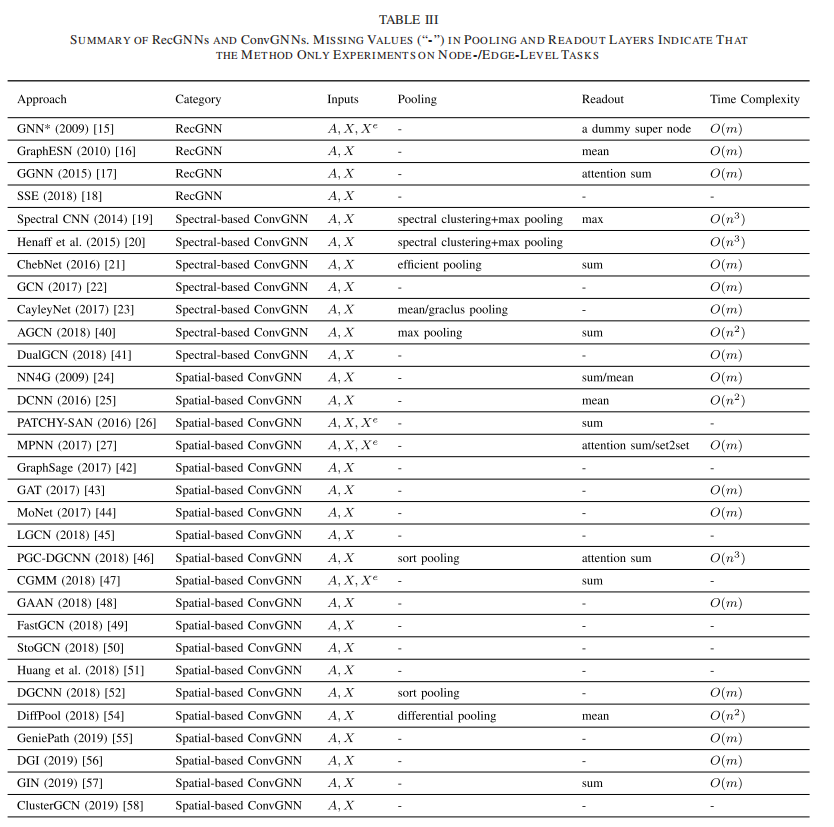
Spatial-Based GCN VS Spectral Based GCN
Spatial-Based: Analogous to the convolutional operation of a conventional CNN on an image, spatial-based methods define graph convolutions based on a node’s spatial relations. The spatial-based graph convolutions convolve the central node’s representation with its neighbors’ representations to derive the updated representation for the central node.The spatial graph convolutional operation essentially propagates node information along edges.
Spectral-Based: Spectral-based methods have a solid mathematical foundation in graph signal processing, based on graph Laplacian. Due to the eigen decomposition of the Laplacian matrix, spectral CNN faces three limitations. (三種局限性) First, any perturbation to a graph results in a change of eigenbasis. Second, the learned filters are domain dependent, which means that they cannot be applied to a graph with a different structure. Third, eigen decomposition requires
computational complexity.
對比兩種方法:
Spectral models have a theoretical foundation in graph signal processing. By designing new graph signal filters , one can build new ConvGNNs. However, spatial models are preferred over spectral models due to efficiency, generality, and flexibility issues. Spectral-based有更好的數學理論基礎保證,而spatial-based更具高效性、推廣性、靈活性。
可用公開資料集
開源GNN庫:
未來研究方向
Model depth: As graph convolutions push representations of adjacent nodes closer to each other, in theory, with an infinite number of graph convolutional layers, all nodes’ representations will converge to a single point. This raises the question of whether going deep is still a good strategy for learning graph data. 一直加深模型的深度對graph類型的數據是否合適,值得探討。
Scalability Tradeoff: 在獲得GNN的scalability時,同時也犧牲了節點鄰居間的影響,結構方面的特征。所以如何均衡scalability和結構特征是一個可能的主題。
Heterogenity:現在研究的GNN都不適用於heterogenity graph,即不適用於有不同類型node和edge的graph。
Dynamicity:現實中graph的node和edge往往是常常變化的,這影響了如何進行graph convolution。
