前言

這幾天都在看SVM相關的內容，SVM的模型在幾何上看上去不是很複雜，但涉及到求解時引入了許多數學概念。這篇總結一下看了一些SVM資料後的想法。

問題引入

SVM考慮如何給一個二分類下的線性分類器更大的Robustness，例如在下邊三個線性分類器中，選擇哪一個將會帶來更好的泛化誤差即。

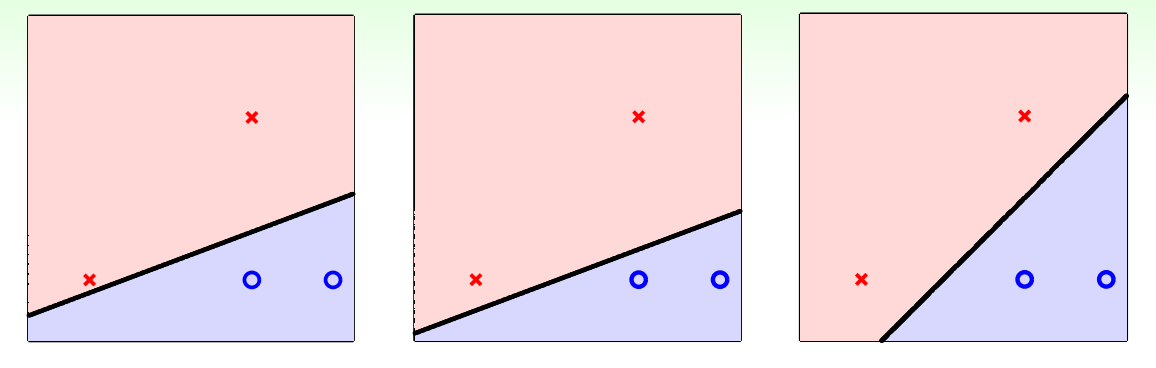
就直覺上來說，我們會選擇第三個模型，因為第三個模型不會過分的貼近某個data point。那麼如何定義這個不過分貼近呢？我們用資料點到直線的距離來表達近的程度，並稱這個距離中的最小值為margin，我們的目標是找到某一個直線(超平面)使得這個margin最大化。使用數學語言來表達即：

上邊的限制(s.t.)是如何來的呢？其實該式是兩種情況下的合併，因為我們的分類器要全部正確分類，所以當時對應，當時對應，所以合併得到。

接下來將高中時學過的點到直線距離公式引入計算這邊的margin得到：

而 ,所以目標式即：

而因為超平面可以進行任意縮放不影響結果，所以可以令,所以目標式轉為：

一般最優化問題我們喜歡用最小化表達，同時引入一個方便後邊運算簡潔，所以目標式轉為：

在問題轉化到這步時，如果data數量不多且維度不高時，可以直接使用QP Solver獲得結果，當數量多且維度高時，我們需要用到下邊的lagrange dual求同解的對偶問題來簡化。