前言

從這篇開始我決定將林軒田老師CSIE5043的內容不以章節的形式記錄，而以分塊的形式記錄。原因一是老師的作業對我來說很有難度（估計要被當了）根本沒時間在周內細緻的整理完一章節的內容，二是希望能在只是塊內提供完整詳細的思路和推導。

問題出發

之前章節的內容是關於如何用線性模型處理分類問題，而我們這邊將更進一步的將其推廣到回歸問題。何謂回歸(regression)問題呢？簡單的來說就是我們的target function的輸出將是實數，對應老師用的notation即:(這邊的(output space)和老師用的字形不太一樣，那個翻遍了都沒找到)。

舉個例子如下圖，某人想要申請一張信用卡，銀行該如何合適的給予其信用積分呢？

我們可以直觀的想到對於申請人的不同背景特征給予不同的權重再加總以評估申請人情況。

將第一column視為feature，第二column為其對應的具體值，這些值構成了訓練集中的

引入模型

與PLA中相類似，我們將作為，讓以簡化模型得到線性回歸的hypothesis如下：

其實這邊和PLA類似，都使用向量內積，只是沒有取改為分類問題而已。

下邊我們用圖示來展現模型與數據之間的關係：

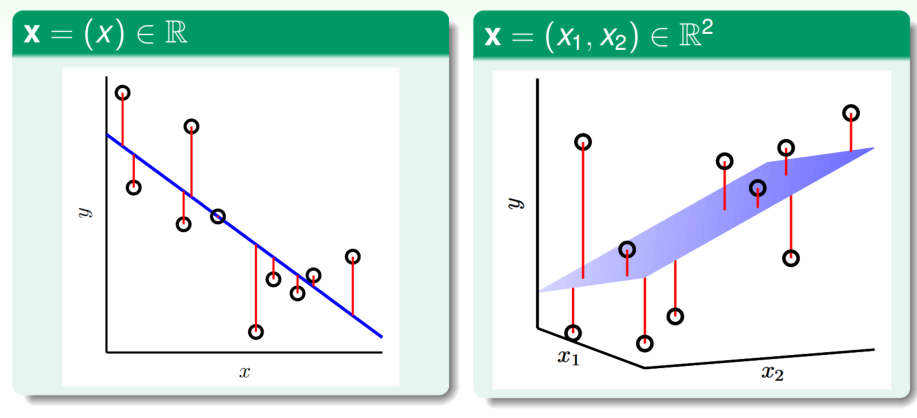
我們的目標是讓一維資料集下的直線hypothesis或二維下的超平面hypothesis與數據點更加貼合，那麼這種理念即對應到如圖中的紅線越短越好。上邊這句話其實就是關於我們如何量化即訓練集內錯誤率。具體到線性回歸問題上，我們常常使用squared error結合pointwise來表達錯誤率如下：

我們訓練的目標是如何最小化再根據之前的理論即能保證即實際應用時的良好效果，接下來將掏出微積分的工具(縫縫補補拿來用)來最佳化訓練集錯誤率

我們的思路是：先將E_in轉為矩陣形式，再對最佳化參數求梯度並令其為0找到極值點。對向量微分 梯度

上邊一串我們推導出了在可逆的情況下，我們獲得令最小的，在不可逆的情況下定義為。這邊的小匕首讀作dagger,而稱作pseudo-inverse（偽逆）,注意可逆情況下的也稱為偽逆。在現實過程中當我們有大量的訓練資料下，常常是可逆的，但實作中老師推薦使用well-implemented routine。

線性回歸算法

  1. from , construct input matrix and output vector
  2. calculate pseudo-inverse
  3. return

線性回歸性質

線性回歸算法看起來並不像一個"Learning"的算法，因為我們在數學上可以直接計算出,並不像有迭代的學習算法。但它可以實際的獲得良好的

下邊用圖表示在線性回歸中資料量與之間的關係

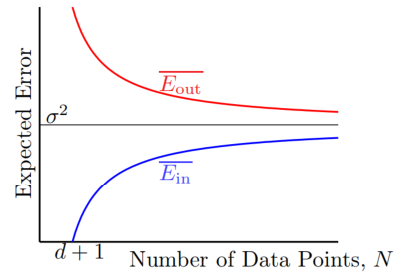
可見在有足夠資料集的情況下，線性回歸能獲得不錯的效果。

參考