上章談到Node Embedding的overview，這次詳細談random walk這一embedding的方法之一。

如同字面上的意思，random walk就是從起始點隨機選一個鄰居節點作為下一個目的地(可以重複走同一edge)，如此往復。

Random-Walk Embeddings

我們的目標是最大化

  1. Estimate probability of visiting node on a random walk starting from node using some random walk strategy

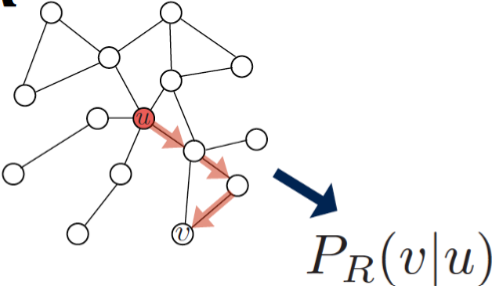
  1. Optimize embeddings to encode these random walk statistics:

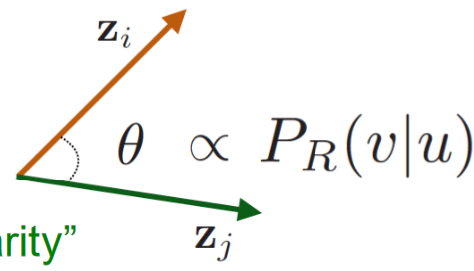
上圖中 越大(即embedding space中此兩向量之間的夾角小)則出現在同一個random walk中的機率越高

Why Random Walks

  • 易表達性：RW靈活多變的定義了node similarity，當從節點走向節點的概率較高時，我們認為兩者的similarity較高
  • 高效性：訓練時不用考慮所有的節點對，僅僅需要考慮出現在同一個RW中的節點對即可。

Feature Learning

接著我們用WR的概念來定義nearby nodes:

neighbourhood of obtained by some random walk strategy

在feature learning中我們的goal是獲得 with ，再通過以下式(式一)評估embedding後同一random walk內node的緊密程度，期望其值越大代表越緊密：

這邊的 是為了讓本身比較小的機率值通過log後放大以促進優化。

依以下步驟具體進行：

  1. Run short fixed-length random walks starting from each node in the graph using some random walk strategy .
  2. For each node collect , the multiset(同一節點可能出現多次，因為可能被重複訪問) of nodes visited on random walks starting from .
  3. Optimize embeddings according to: Given node , predict its neighbors

而式一等價於式二：

接著為了讓節點之間的相似度更高，套用softmax函數：

代入式二則得到式三:

最佳化RW embedding即找到使得最小的

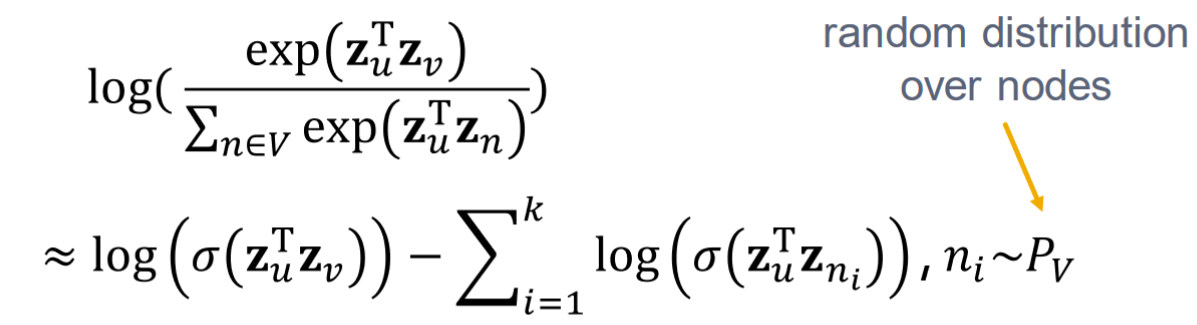
因為式三需要遍歷兩次整個graph，即複雜度為過高，所以我們採用一種Negative Sampling的方法來降低複雜度：

為什麼這樣的近似可以降低複雜度可參考: Negative Sampling

優化了複雜度後，我們回到主要的任務(即找到使得最小的)，這邊使用到的方法是Stochastic Gradient Descent(SGD)，這部分移步：

GD

SGD

Node2vec

上邊我們談到的是一種簡單的random walk策略(deep walk)，即fixed-legth&unbiased。接下來提到的node2vec方法將更加豐富。

Key observation of Node2vec: Flexible notion of network neighborhood of node leads to rich node embeddings.

node2vec在如何選擇這件事上更加靈活多遠，帶來更多的embedding可能性。

在如何選擇上，node2vec提供了兩種經典策略，即BFS和DFS：

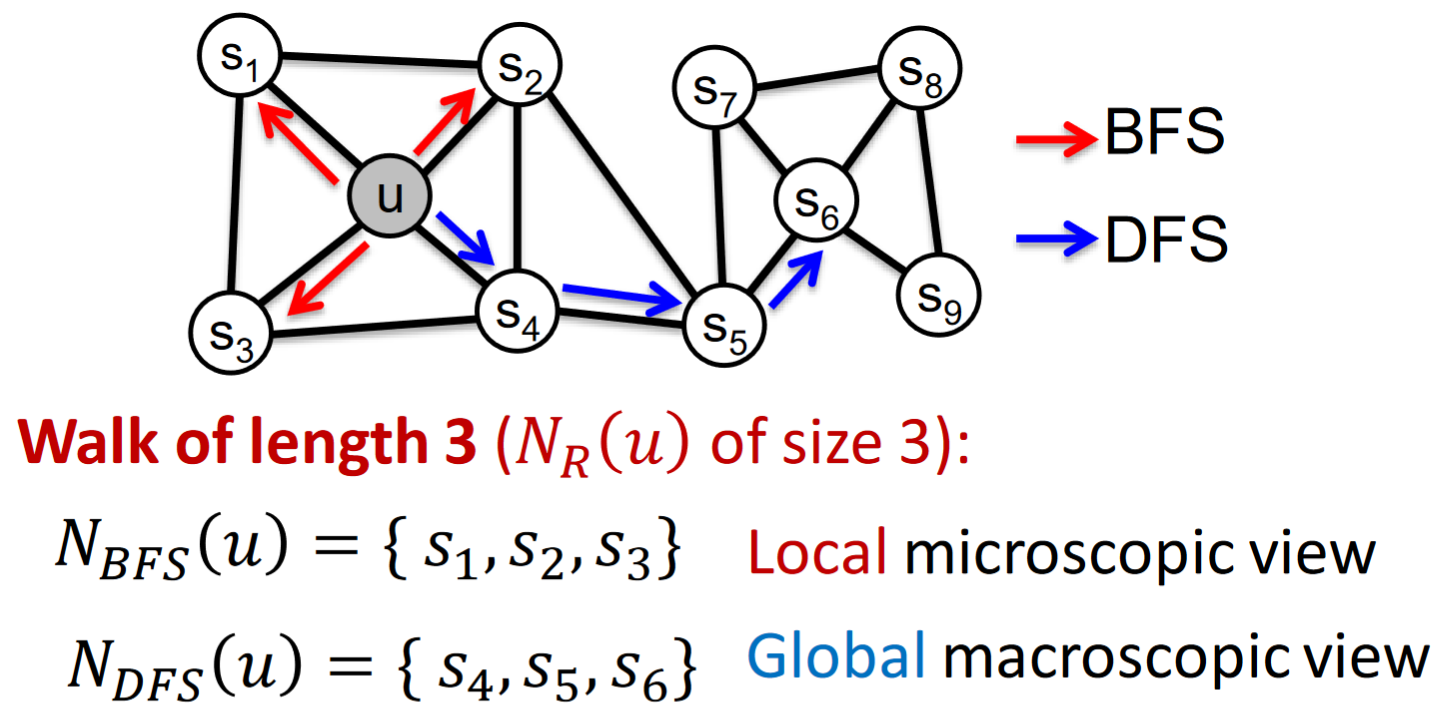
如何達到BFS和DFS兩種形式的遊走呢？考慮使用兩個參數來實現： * : 返回上一個node的機率 * : 選擇BFS還是DFS之機率比

這種形式叫做：Biased -order random walks，因為其知道上個走過的節點。

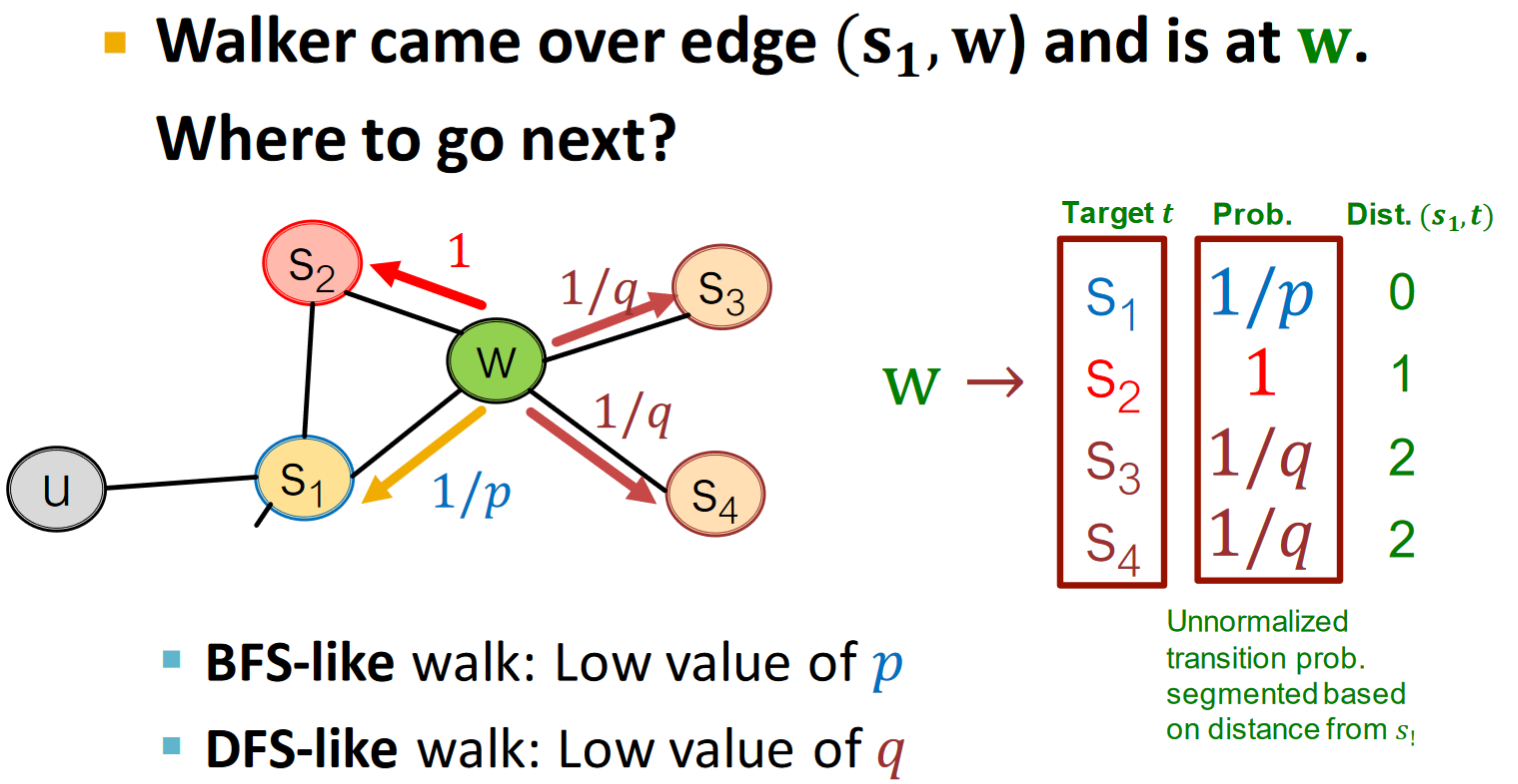
遊走從走到下一步如何被兩個參數影響如上圖所示。

Node2vec algorithm(三者可平行進行): 1. Compute random walk probabilities 2. Simulate random walks of length starting from each node 3. Optimize the node2vec ovjective using SGD

參考

  • https://medium.com/@st3llasia/graph-embedding-techniques-7d5386c88c5
  • http://web.stanford.edu/class/cs224w/