Effective Number of Lines

以下討論時，ML是否可行。考慮以下條件:

即如下圖所示：

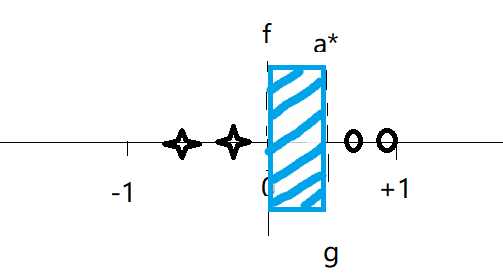
可見與圖中處時，而由藍色區域結合uniform distribution的CDF判斷 。

令 即

即只要，會大於設定的threshold。

所以:

這邊我們的有無數多個,可見即使無限大時，仍有較小機率出現BAD DATA。

上一篇文章我們提到下式(式一)：

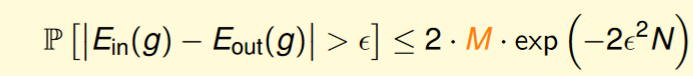
該式子的產生是建立在我們計算union bound作和：

這邊是是因為我們可能有相似的hypothesis對BAD event重複了，即如下圖所示：

以下我們將討論如何統計overlap的情況(使用對hypothesis分組的形式)：

如上，考慮𝟚中的一個特征向量，我們可以根據該點將平面中的直線(hypothesis)分為兩類：一類將歸為circle，一類將其歸為cross。

接著我們將上面推廣(N代表hypothesis分類個數):

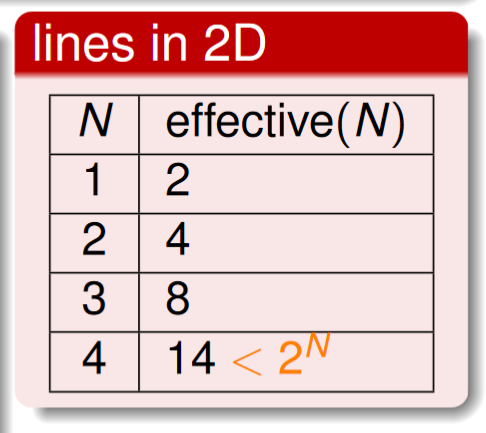
將上邊的式子代換為有限的hypothesis數(effective(N))如下：

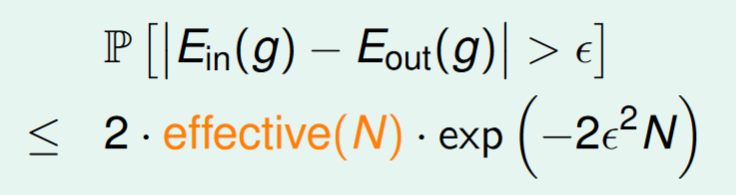
所以滿足以下兩個條件則Learning possible with infinite lines：

  1. can replace

Effective Number of Hypothesis

接上來將上邊討論的直線情況推廣到任意形式的hypothesis

我們定義dichotomy(二分法)如下：

接著我們將應用到得到很多不同(經過去重)的dichotomy。如下圖總結：

以上我們得到的將作為替代式一中的選項