Infeasibility of Learning

All learning algorithm has its assumptions behind. No algorithm is best for all learning problems.

上圖中 對於data set中的所有個例都成立，而這些對於data set以外的卻不能保證。可見這種機器學習無法保證資料集以外的準確性，這顯然不符合我們ML模型的應用場景，因此引出以下內容完善這一缺點。

Inferring Something Unknown with Assumptions

對於一個有兩種顏色小球的罐子，我們一開始並不知道橙色小球的佔比。所以我們嘗試用sampling的assumption(training data& test data is related by a distribution)來做估計:

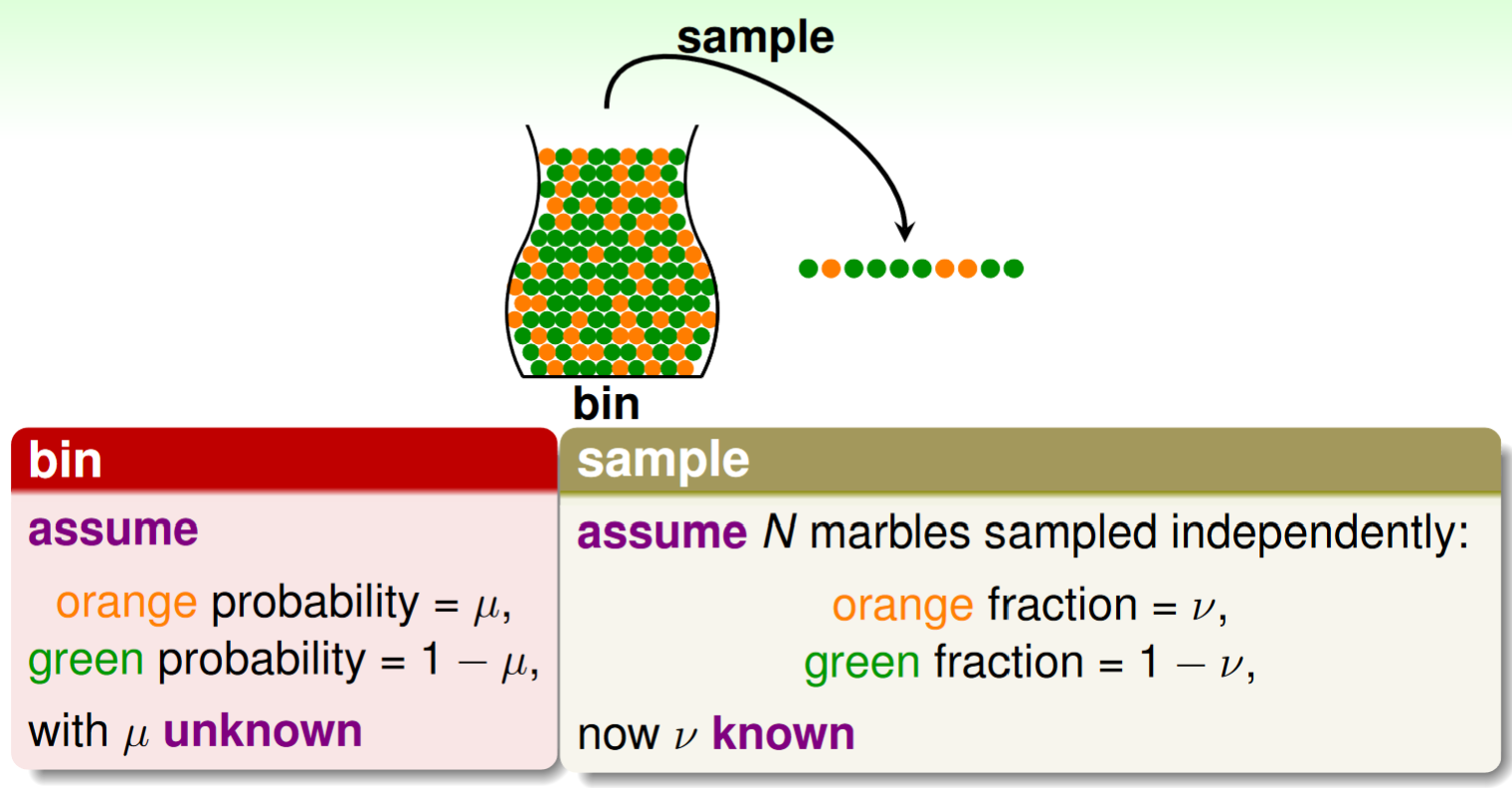
但是以上採樣和結果並不能完全保證體現罐子內的顏色真實分佈，但在樣本數足夠大時，可以達到 Probably Approximately Correct(PAC) under iid sampling assumption.

independently identically distribution(i.i.d.): In probability theory and statistics, a collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent. --- Wikipedia

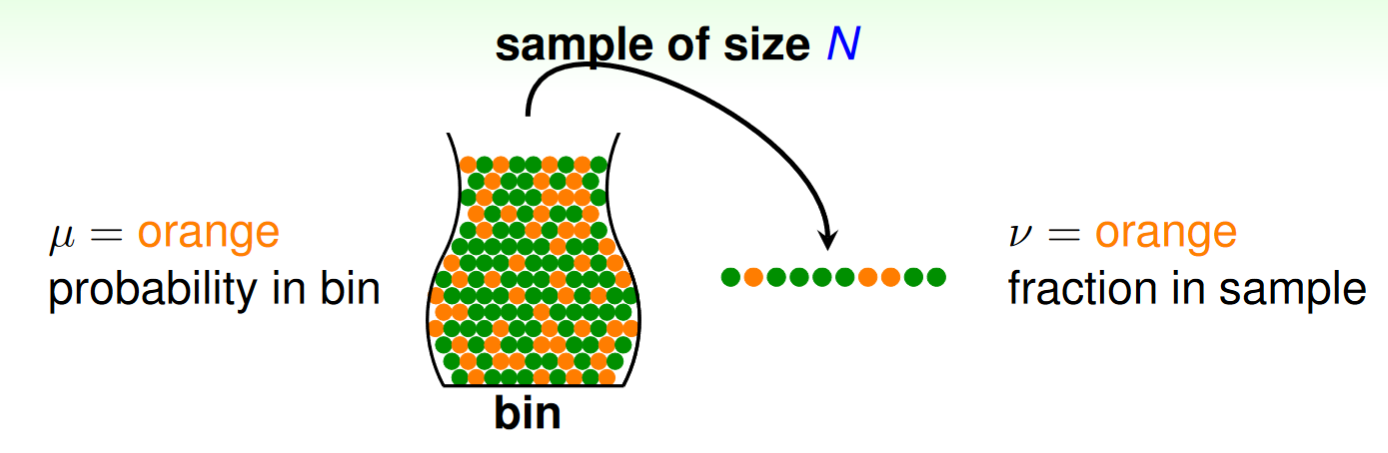
上圖中和滿足 Hoeffding's Inequality(即樣本足夠大時可以通過取樣達到PAC):

其中是指我們設定的threshold

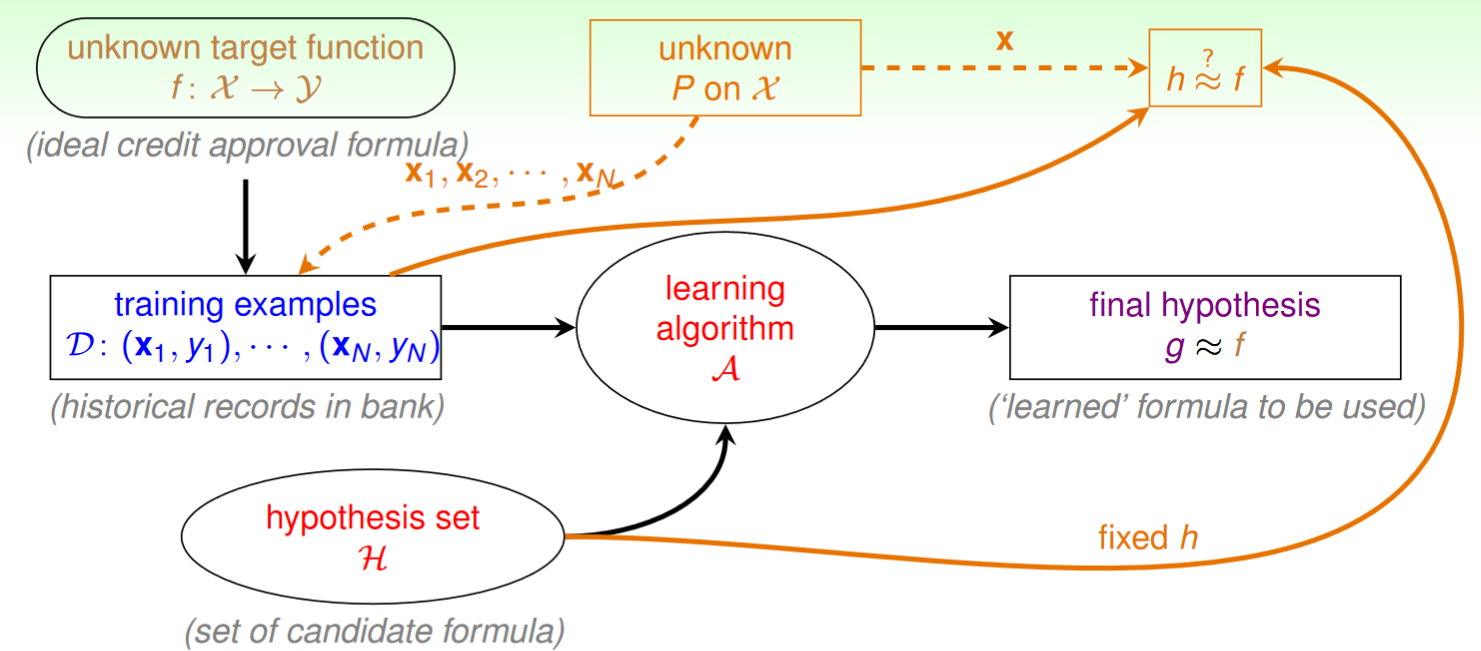
Connection to Learning(Verification)

接下來，我們將上述的罐子例子與ML聯繫起來。

  • 橘色球佔比的未知性 = 某hypothesis是否為targer function的未知性
  • 罐子中的球 = Input space中的Data set
  • 球是橘色 = 某hypothesis不是targer function
  • 球是綠色 = 某hypothesis是targer function
  • 從罐子中取出N個樣本採樣 = 用Data set判斷是否

if large and i.i.d., can probably infer unknown probability by known fraction.

當樣本數足夠大且資料集iid時，可以大致用資料集驗證下的某hypothesis錯誤機率推測客觀上真正未知的該hypothesis是否為target function的機率。

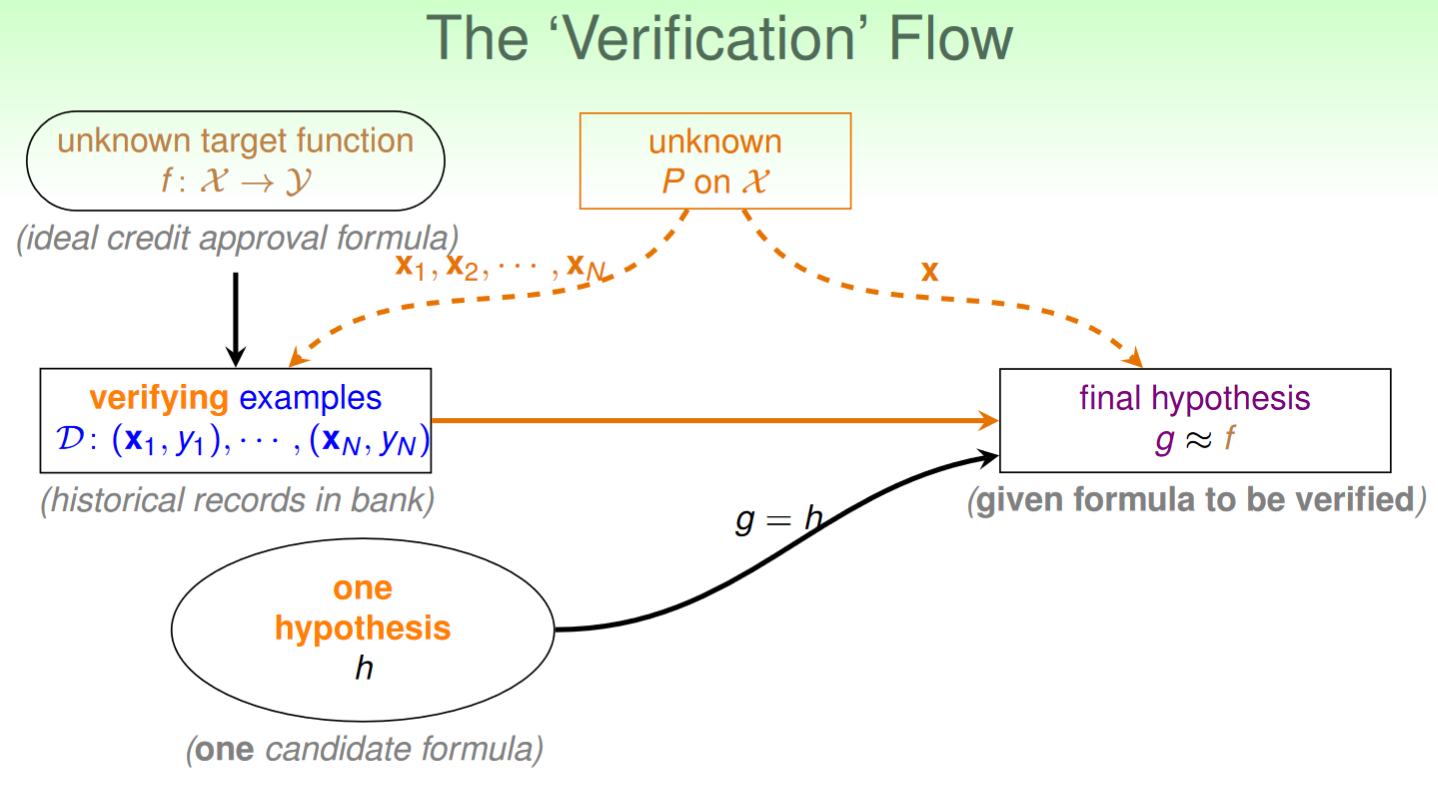
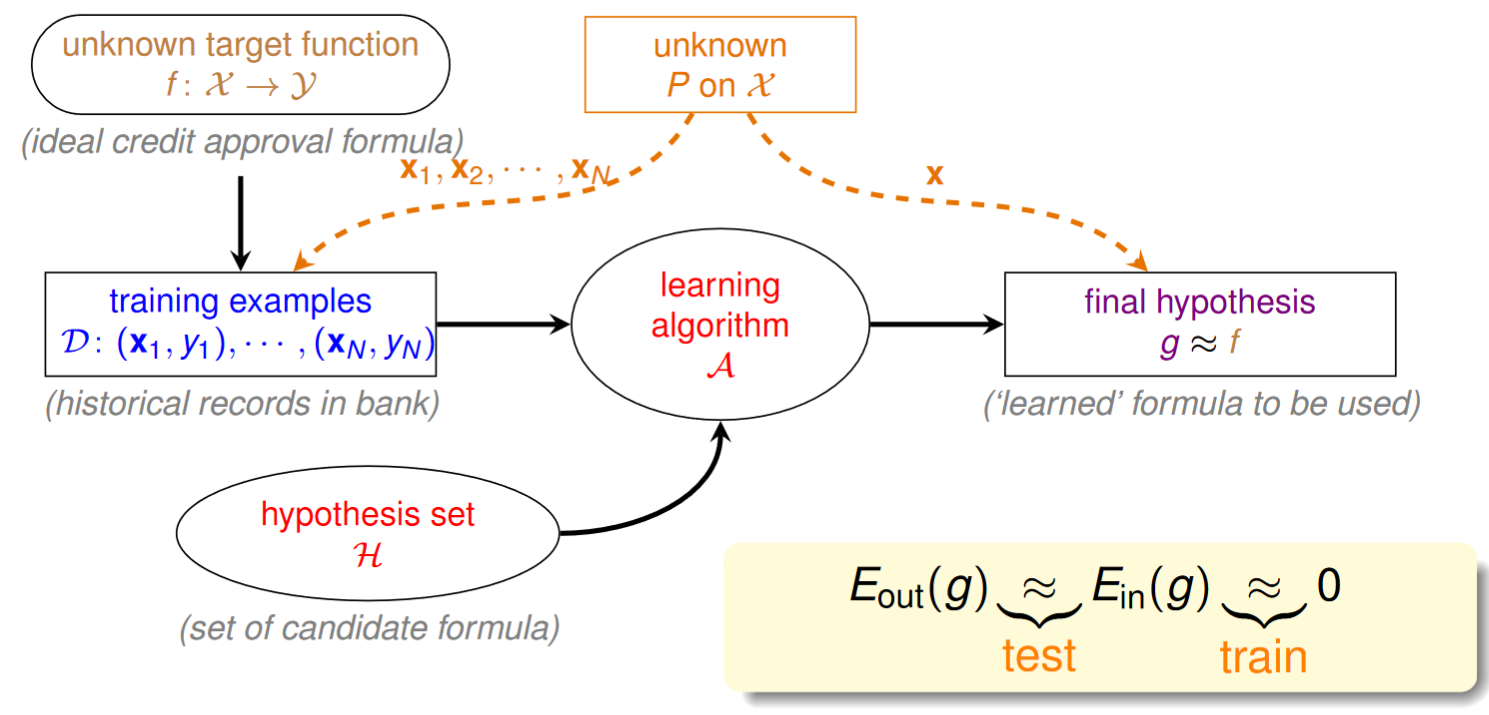
將以上的概念加入ML流程圖中得到:

for any fixed , can probably infer (under iid sampling assumption)

unknown , same as error rate

by known

in-sample error is probably close to out-of-sample error

is PAC

以上推論可以得到:

if and is small

is small

with respect to

即在樣本夠多且某hypothesis在data set測試下錯誤率足夠低的情況下，該hypothesis近似於target function

但上邊的推論都建立在我們只給予計算機一個hypothesis的情況下，所以基本上計算機也只能被迫強制接受這個hypothesis，也許不能足夠小且 PAC。所以這種方法只能作為驗證某單一hypothesis是否合適的流程，如下圖:

Connection to Real Learning

BAD Data: and far away

Hoeffding不等式保證了在data set數量足夠多時，對於某hypothesis出現BAD data set的機率很低。

當面對多個hypothesis和多個data set(DS)的情況時，我們假定某DS對任一hypothesis是BAD則稱該DS為BAD，反之為GOOD。

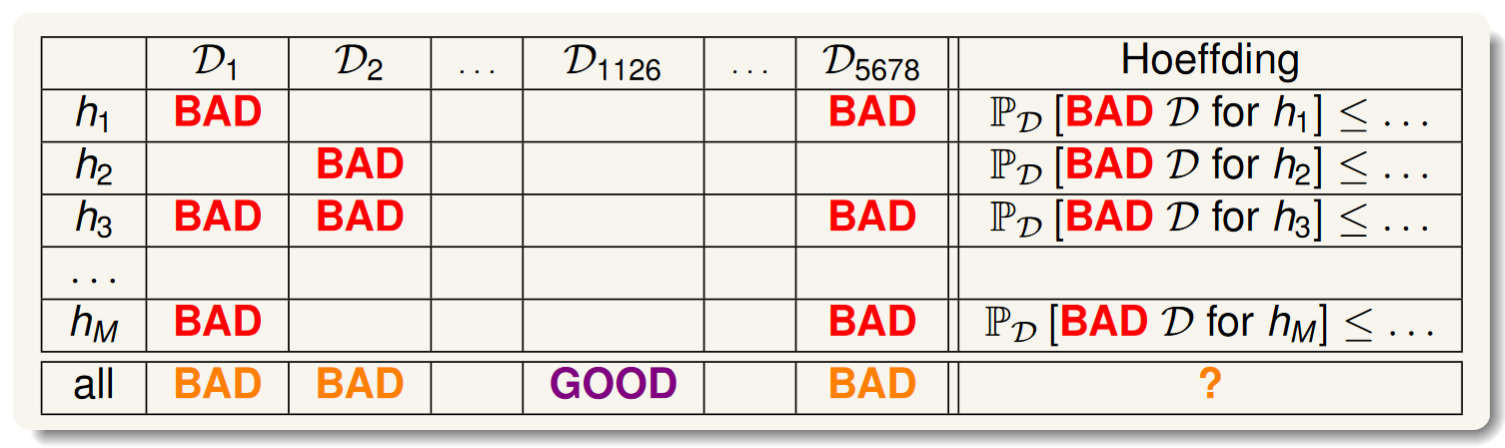
我們推得所有hypothesis的bad data set機率如下:

M is Num of hypothesis in hypothesis set.

這保證了其機率被限制在較小範圍內， for any is PAC, regardless of

most reasonable (like PLA) pick the with lowest as .

Feasiblity of Learning Decomposed

通過以上推論我們總結出以下關鍵內容:

在hypothesis數量有限的情況下，當足夠大時，無論Learning algorithm取到任意hypothesis ，都有

當Learning algorithm找到 with 時， PAC被確保

即 , 即可以通過訓練和assumption的機器學習是可行的。

接下來引出ML理論的兩個重要問題：

  1. Can we make sure that is close enough to ?
  2. Can we make small enough?

我們從hypothesis set with 的角度來看這個問題如下：

  1. 候選hypothesis少(即M小)時，問題1可以得到保證，因為,而問題二無法得到保證因為我們候選的hypothesis較少
  2. 候選hypothesis多時，情況與上反之。

可見，對hypothesis set的大小把握是一件重要的事

參考

  • https://en.wikipedia.org/wiki/Independent_and_identically_distributed_random_variables
  • https://www.csie.ntu.edu.tw/~htlin/course/ml21fall/