Goal: We want features that characterize the structure of an entire graph
Background: Kernel Methods
Idea: Design kernels instead of feature vectors.
What is kernel:
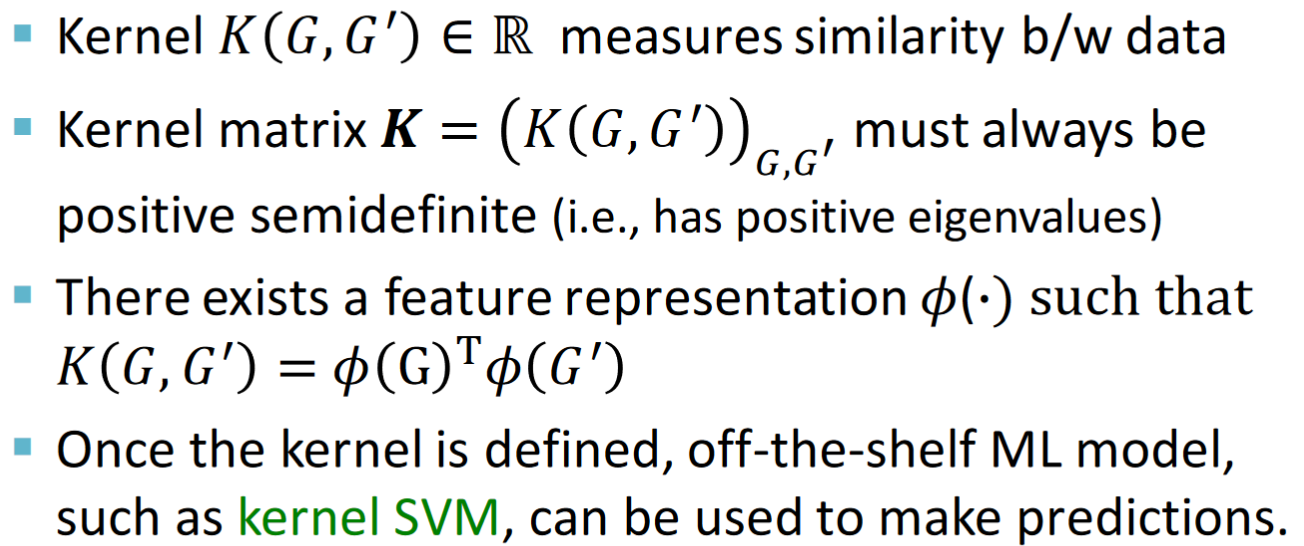
TODO:kernel詳情
Graph Kernels
Graph Kernel: Measure similarity between two graphs
Goal: Design graph feature vector
Key idea: Bag-of-words(BoW) for a graph

假如簡單的將nodes當做words那麼如上圖將很容易造成對不同的圖提取出相同的feature vector。所以嘗試用node degree來提取feature vector,如下圖:
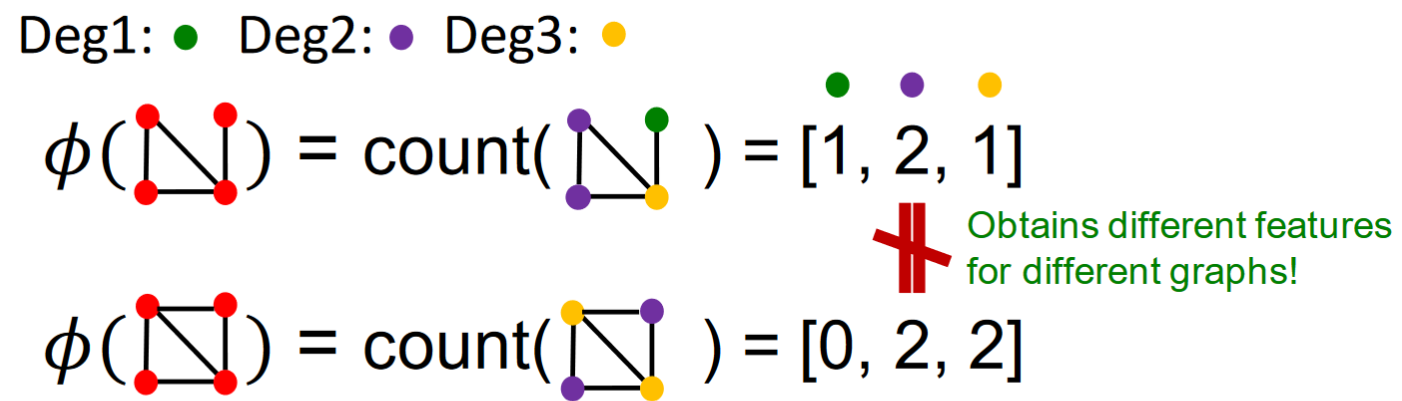
Both Graphlet Kernel and Weisfeiler-Lehman(WL) Kernel use Bag-of-* representation of graph, where * is more sophisticated than node degrees.
Graphlet Kernel
key idea: Count the number of different graphlets in a graph
注意:這邊的graphlet和node-level feature中提到的有些許不同。
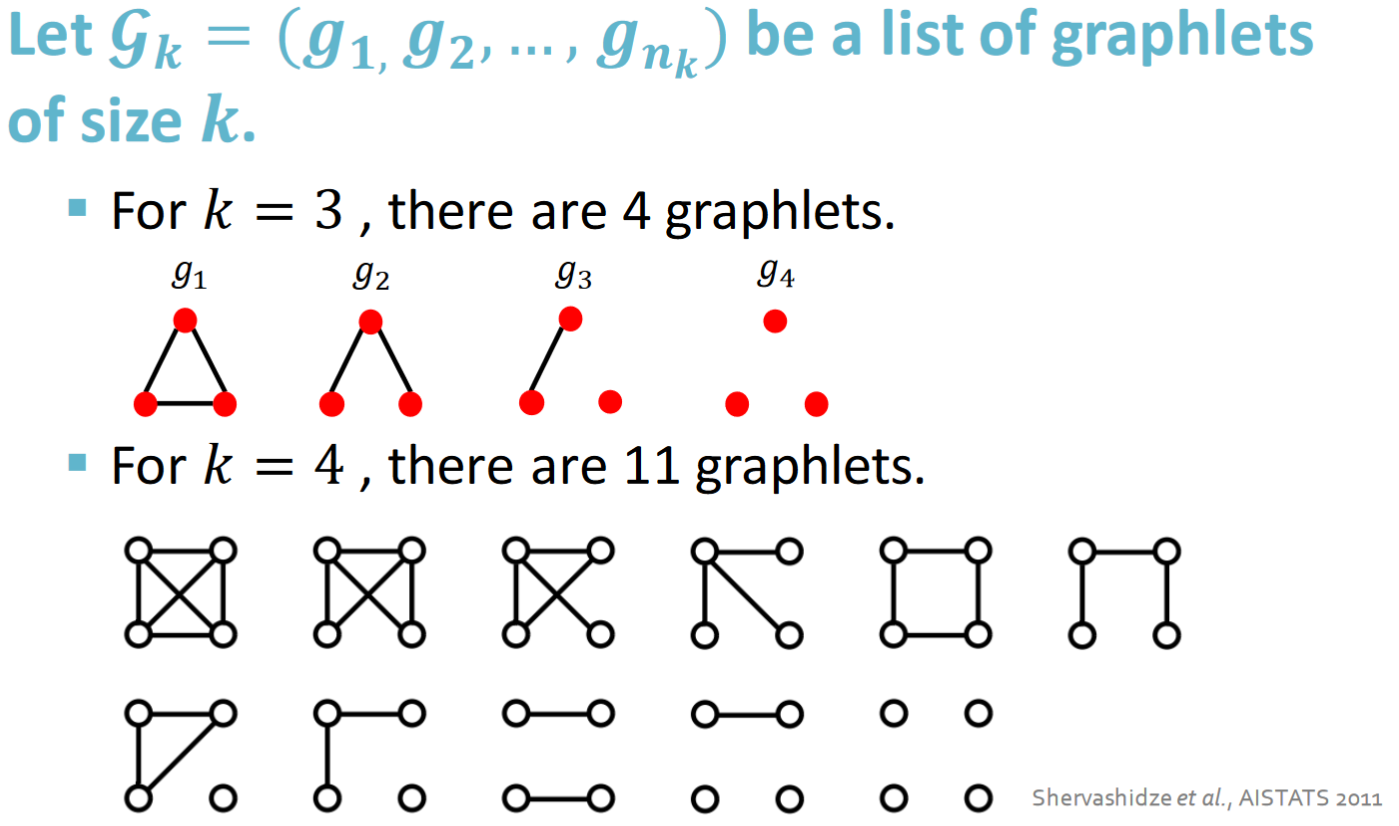
Given graph
, and a graphlet list , define the graphlet count vector(GCV) as # for 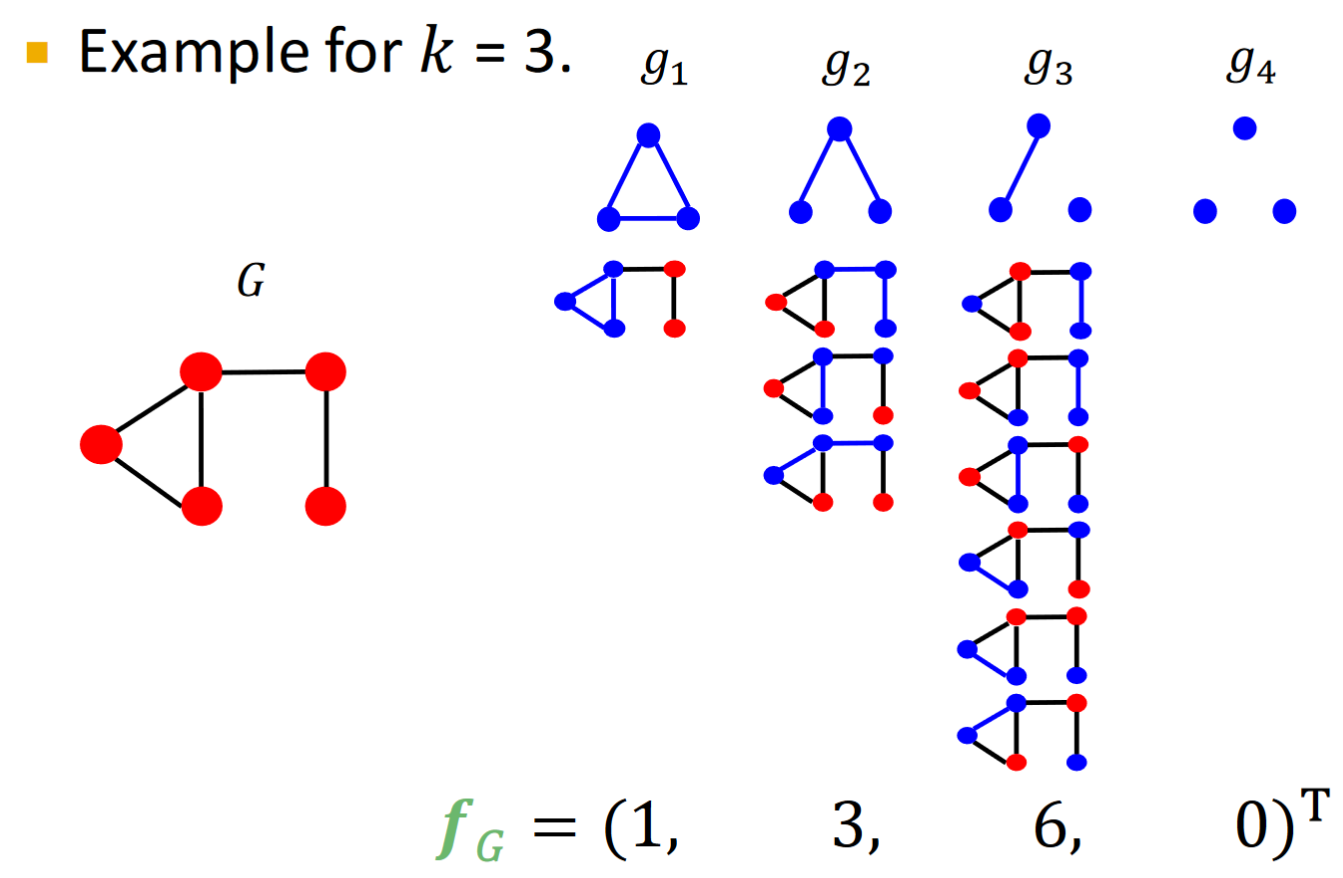
Compute graphlet kernel:
Given two graphs,
and , graphlet kernel is computed as 計算graphlet kernel時可以用
的GCV的轉置矩陣dot product上 的GCV得到。但當兩個graph的size不同時結果會發生偏差,所以使用以下方法normalize: 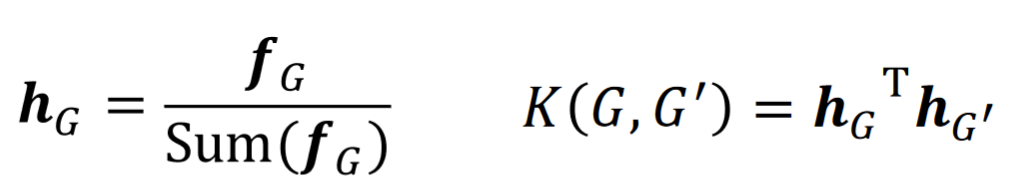
Limitations: Counting graphlets is expensive.
Graphlet kernel的局限性在於對graphlet的計數所花的計算成本非常高。
Weisfeiler-lehman Kernel
Goal: design an efficient graph feature descriptor
Idea: use neighborhood structure to iteratively enrich node vocabulary.
Algorithm to achieve this: color refinement
Color Refinement:

e.g.
將節點以其鄰居節點情況進行合併 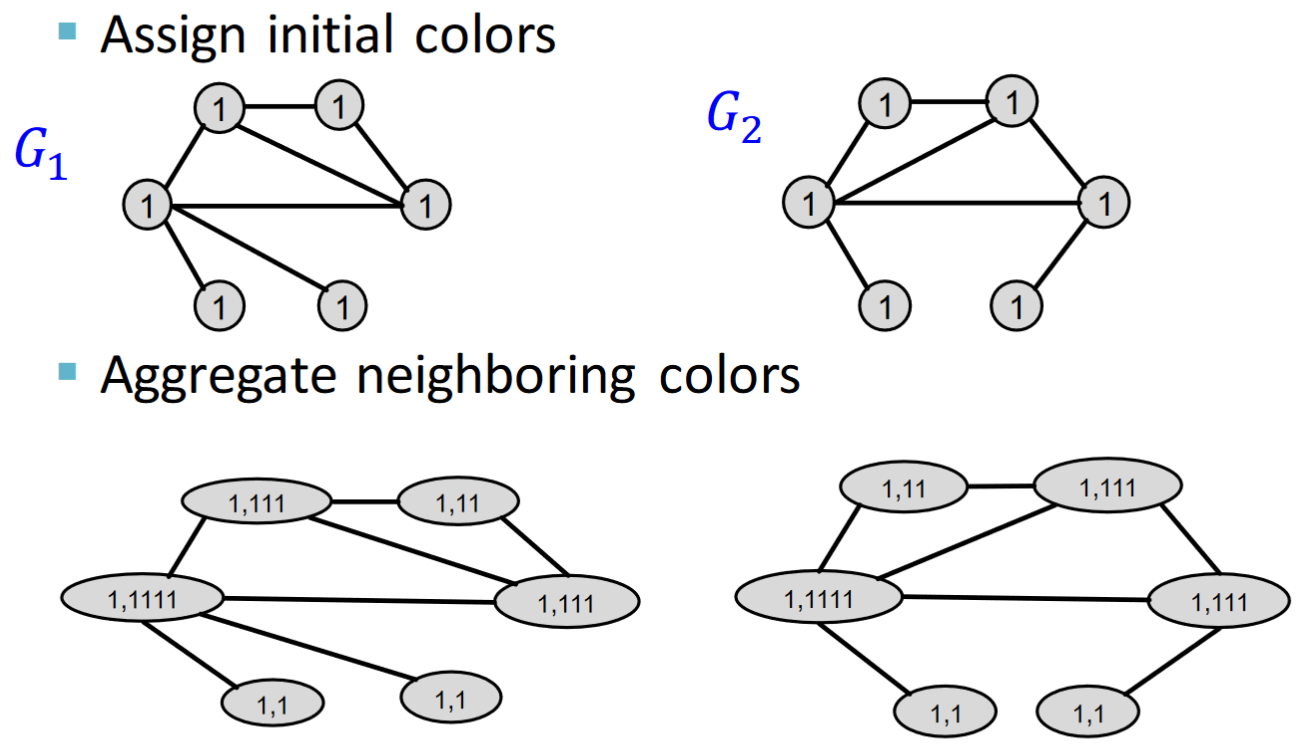
應用hash table: 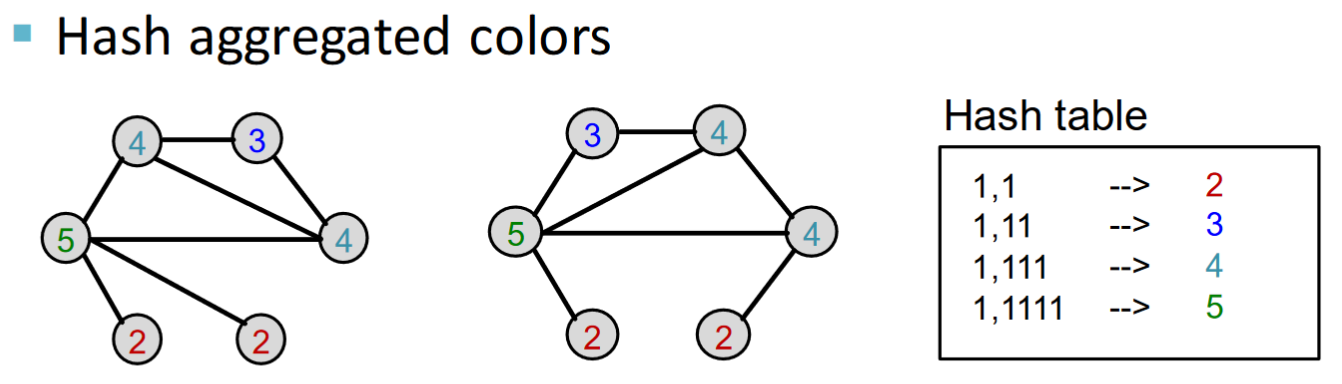
再進行合併: 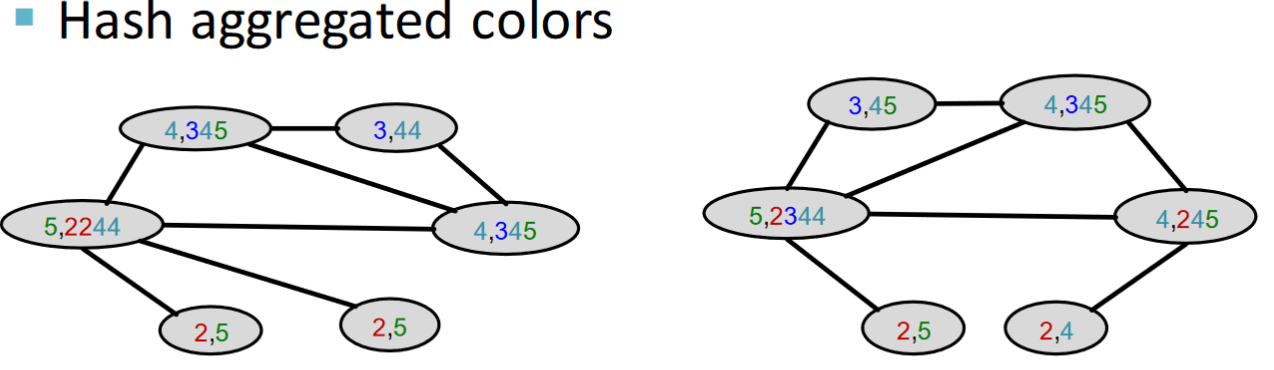
再進行hash: 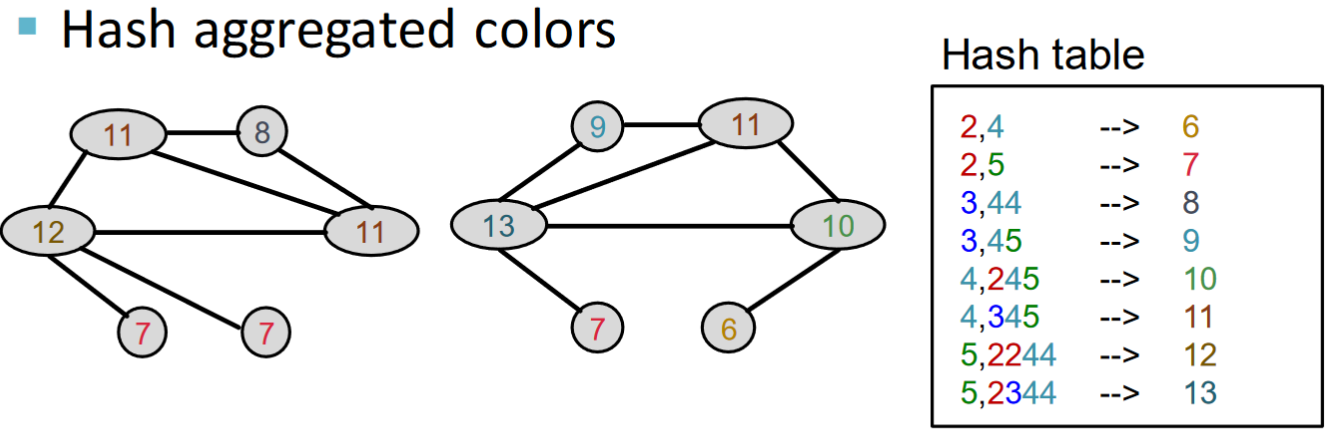
以(hash-合併)步驟持續迭代,而後WL kernel統計不同顏色的數量形成顏色向量(11 12 13似乎有勘誤):
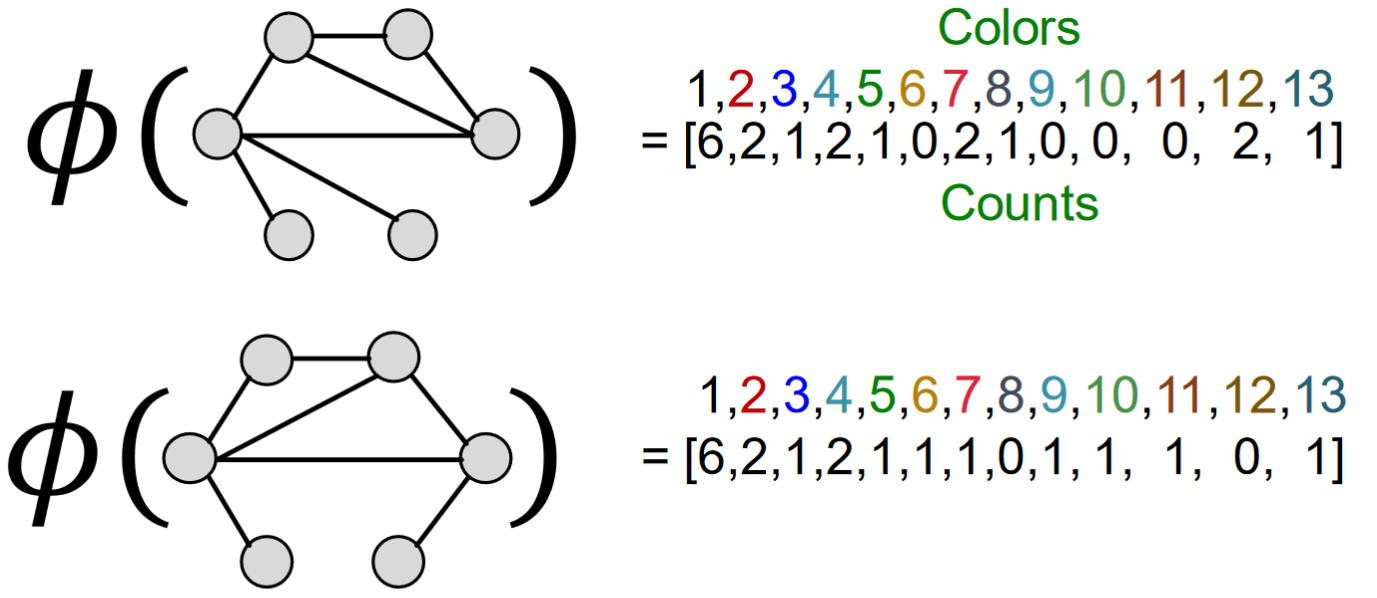
接著計算兩個向量的inner product即得到WL Kernel value:
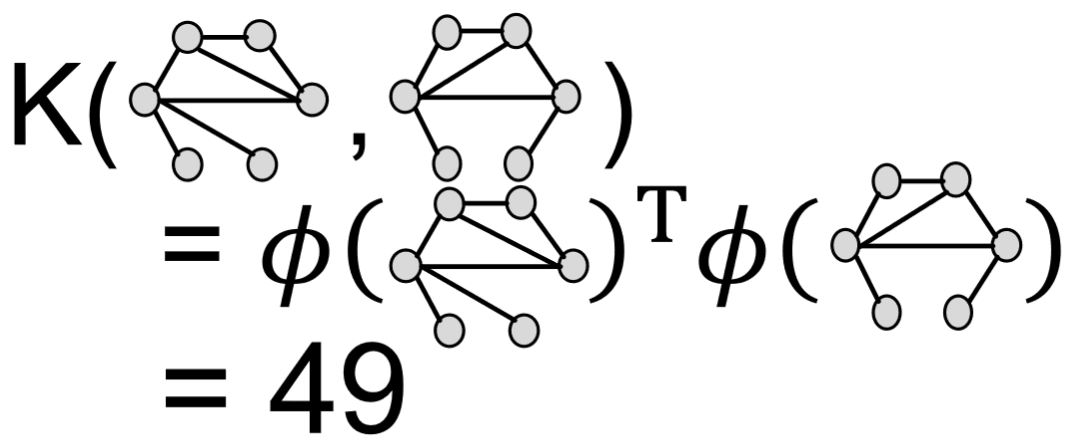
WLkernel在計算上是非常高效的,其複雜度與節點數量呈線性關係。
參考
- http://web.stanford.edu/class/cs224w/
- https://github.com/holgerdell/color-refinement
