Link-level Prediction: predict new links based on existing links.

The key is to design features for a pair of nodes. >

  1. links missing at random

Remove a random set of links and then aim to prediction them.

隨機去除graph中的一些link然後嘗試用機器學習找回這些失去的link

  1. links over time(隨著時間來預測)

Given a graph on edges up to time , output a ranked list of links(not in ) that are predicted to appear in

當我們有一個隨時間變化的graph時(如Citation network等)，我們使用來預測的Link情況。

評估的方式即用預測將出現的link和實際出現的link情況對比。

Methodology：

  1. For each pair of nodes compute score ，例如用的共同鄰居節點數來計算score
  2. Sort pairs by the decreasing score
  3. Predict top pairs as new link
  4. See which of these links actually appear in

  1. Distance-based feature

    Shortest-path distance(SPD) between two nodes

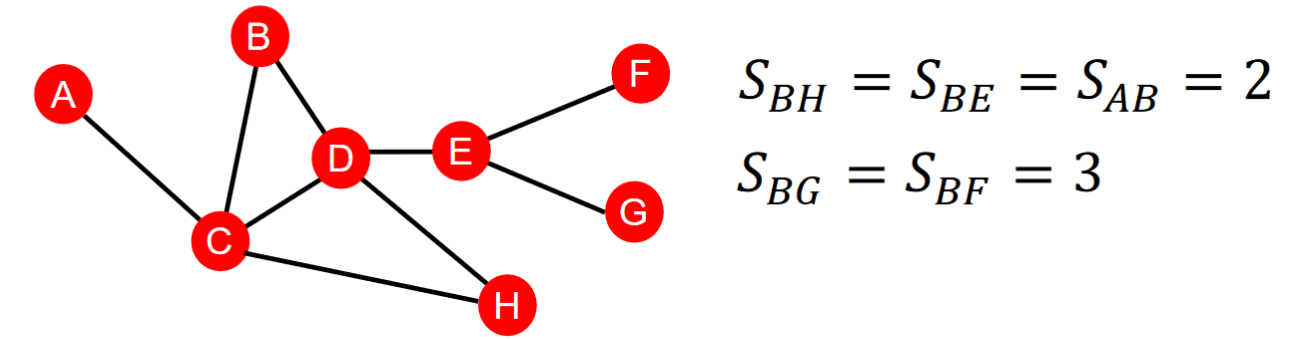
這種方式很自然直接但無法表示連接的強度，如BH(可通過C或D)之間的連接強於BA但他們的SPD一樣。

  1. Local neighborhood overlap

    Captures Num of neighboring nodes shared between two nodes and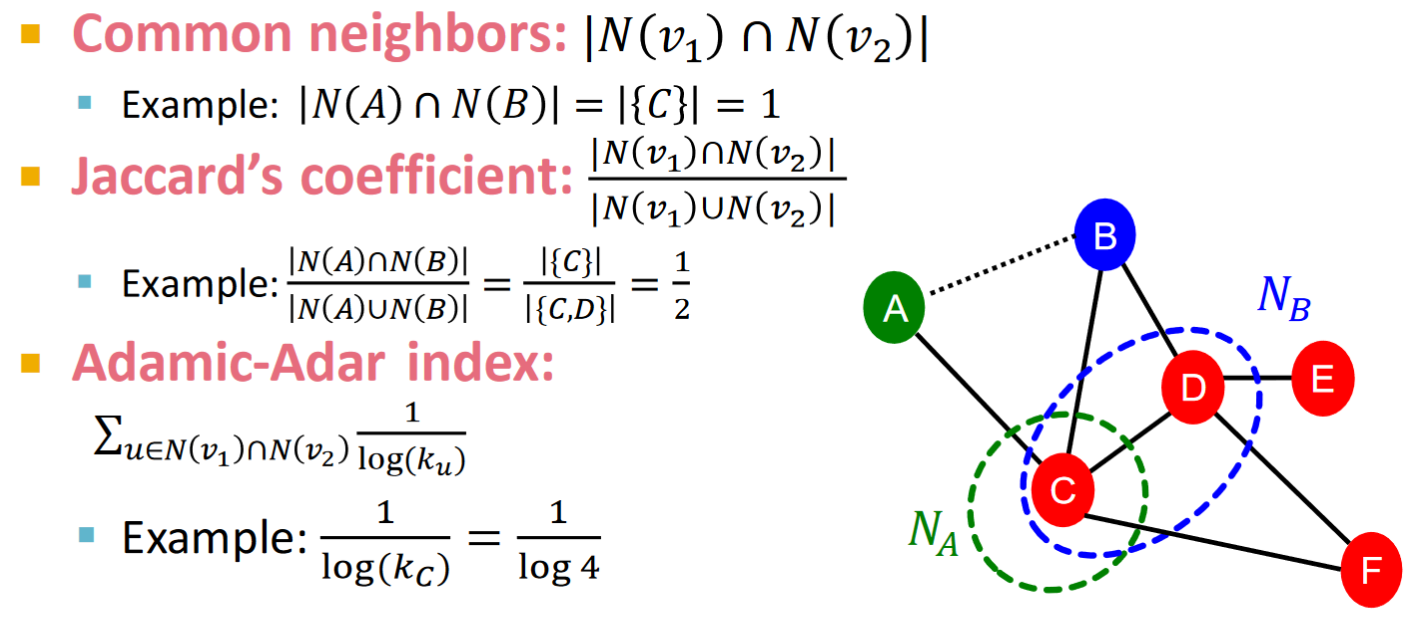

    表示的所有鄰居節點集合。

    Jaccard's coefficient是共同鄰居節點數相對於兩者共同degree的平均標準化，否則高degree的node之間的link strength將顯然更強。

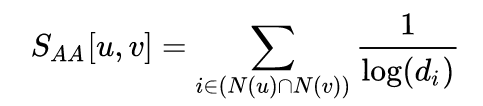    AA賦予了低degree的common neighboring nodes更高的權重，通過取對數後再取倒數的模式。

  2. Global neighborhood overlap

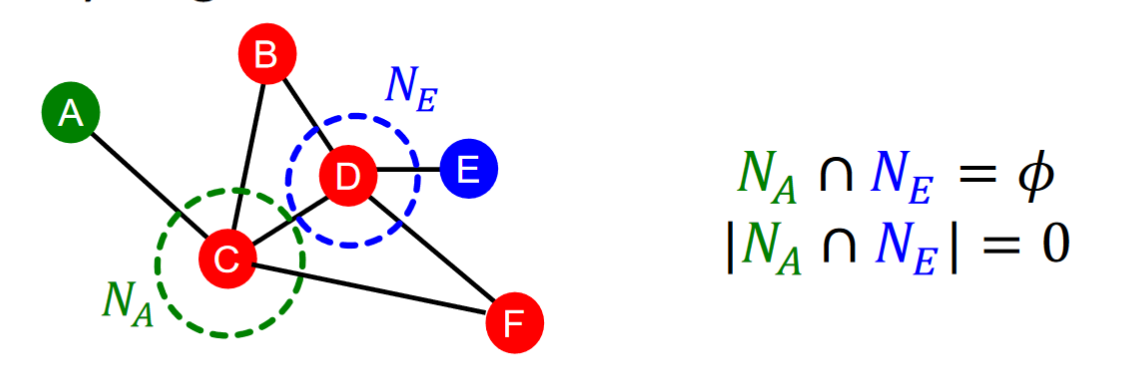
    Local neighborhood overlap的缺點在於距離兩步以上的兩個節點沒有common neighbor那麼其衡量標準得到的結果都將為0，但我們不能說這兩個節點之間的link strength為0。因此我們需要定義Global neighborhood overlap。

    Katz index: count the num of paths of all lengths between a given pair of nodes. 統計兩節點間的所有path數，不論其長度。這個index可以使用鄰接矩陣的power計算得到，如下:

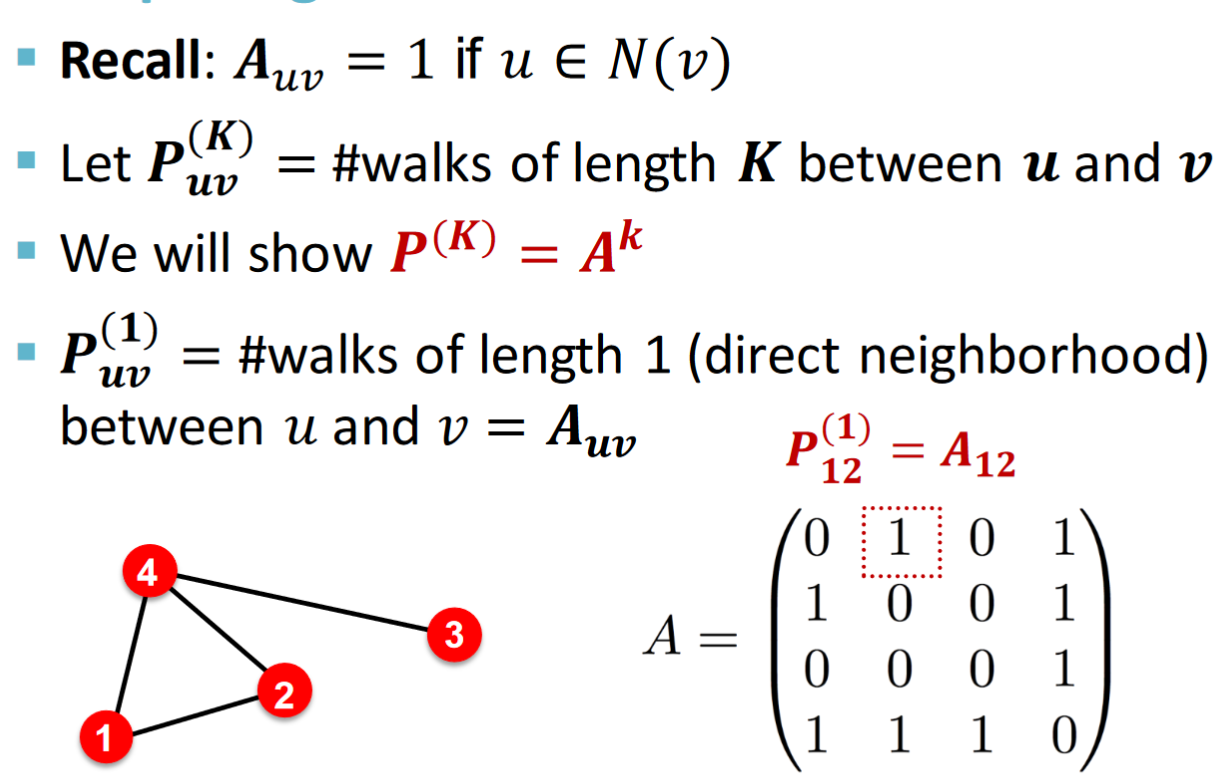
    即計算節點間某長度的path數可以簡化為求鄰接矩陣的長度冪次。所以計算所有長度path數之和時得到以下公式：

    用來降低長路徑的影響程度。

參考

  • http://web.stanford.edu/class/cs224w/