Motivation
We wanna be able to create additional features that will describe how this particular node is positioned in the rest of the network, and what is its local network structure and these additional features that describe the topology of the network of the graph will allow us to make more accurate predictions.
SO this means that we will always be thinking about two types of features. Structural features, as well as features describing the attributes and properties of the nodes.
Traditional ML Pipeline
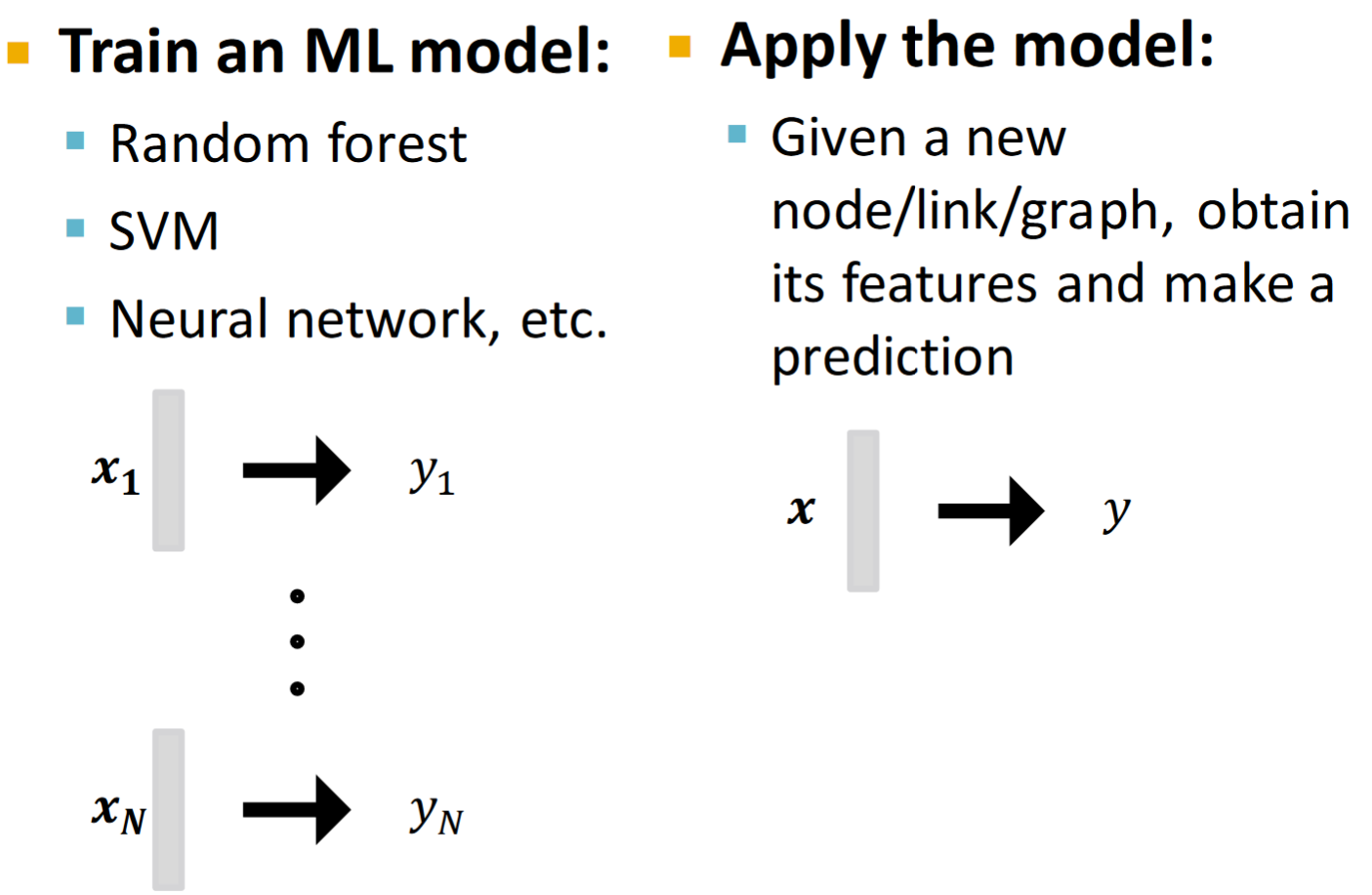
首先,我們將nodes乃至整個graph使用特征向量來表達。接著訓練一個傳統的ML模型,例如SVM、neural network等。這樣該模型就能完成未來的預測任務。
Node Features
傳統ML使用的是hand-designed feature(手動設計的特征)
- Node degree
之前介紹過,代表節點連接的edge數。這種feature的缺點在於無法提供節點在graph上的未知信息,邊緣節點和中心節點可能被視為擁有相同feature。
- Node centrality(中心度)
節點中心度表達了某節點在graph中的重要性。可供選擇的中心度表達方式有: Eigenvector centrality/Betweenness centrality/Closeness centrality等
Eigenvector centrality
A node
is important if surrounded by important neighboring node
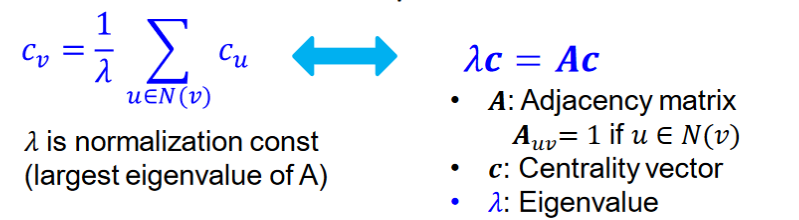
當某節點周圍節點的centrality越高時,該節點也相應的中心度越高。
Betweenness centrality
A node is important if it lies on many many shortest path between other nodes.
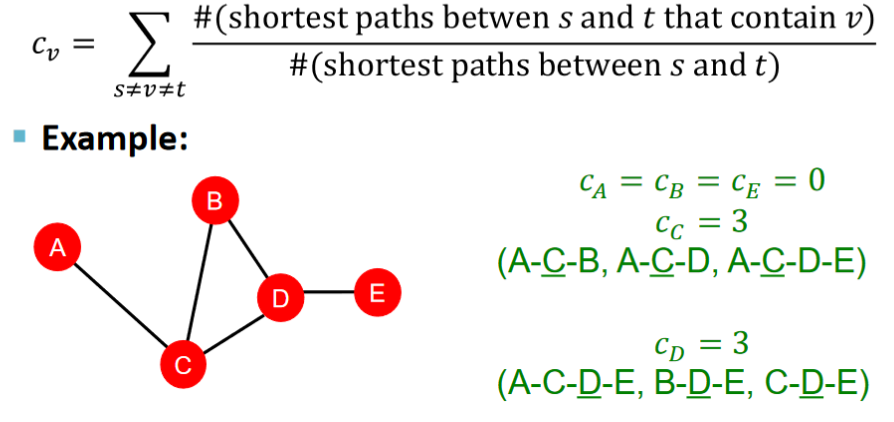
當某節點在不同節點溝通path中頻繁出現時,該節點的centrality越高。這類似一個交通樞紐的概念。
Closeness centrality
A node is important if it has small shortest path length to all other nodes.
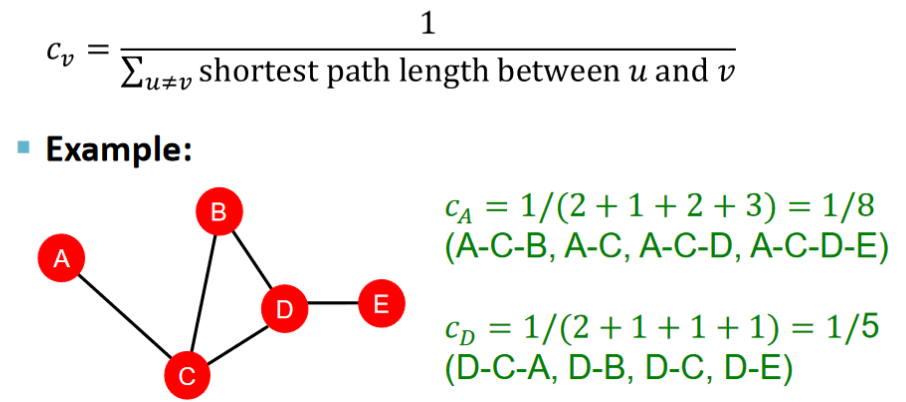
某節點到graph中其他節點的路徑和越短時,其centrality越高。
- Clustering coefficient
Measuers how connected
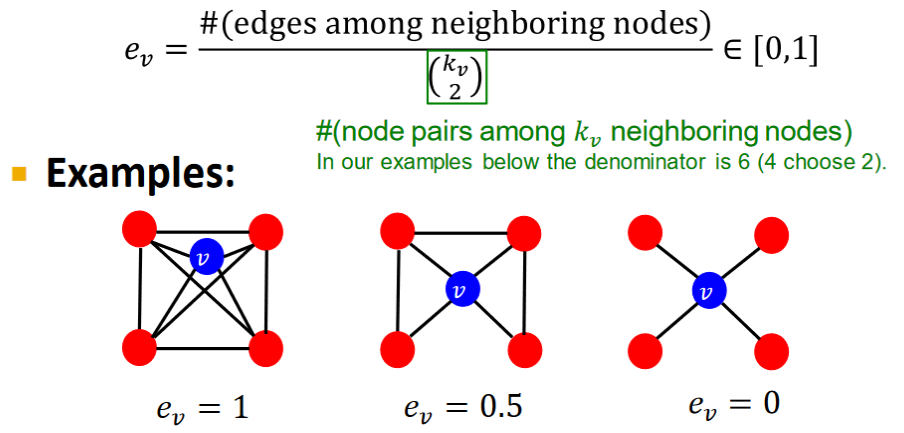
即用某nodes的鄰居nodes實際edge個數除以理想情況下的最大edge數,該係數表達了某節點對連通身邊的貢獻度。
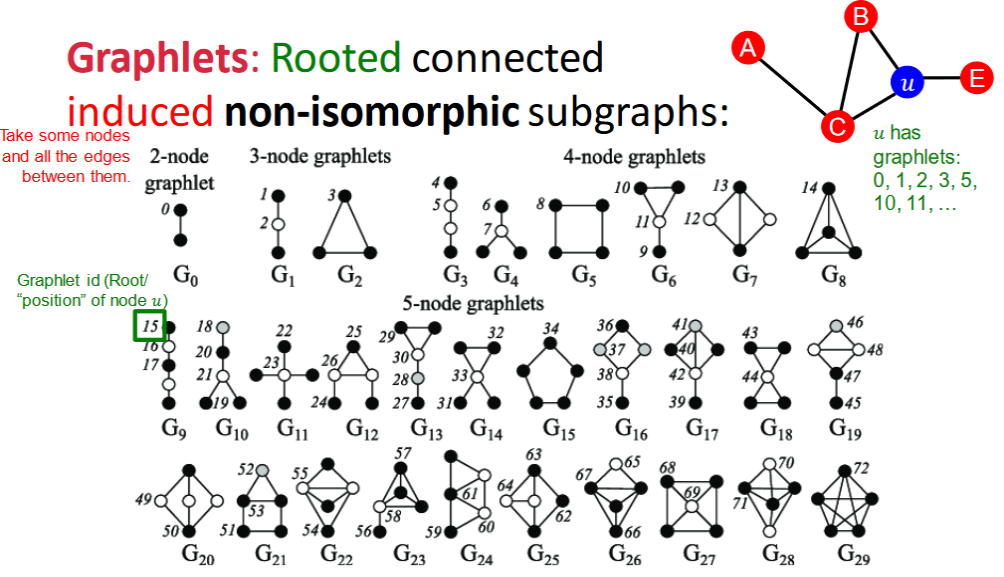
- Graphlets
Observation: Clustering coefficient count the triangles in the ego-network.
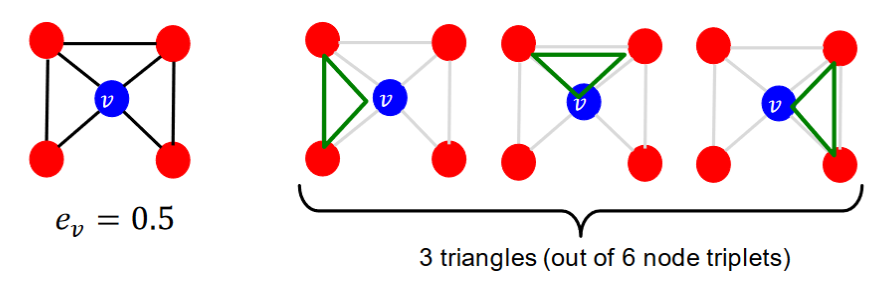
Def:
Graphlets: Rooted connected non-isomorphic(非同構) subgraph
Graphlets are small subgraphs that describe the structure of node
's network neighborhood. Graph Isomorphism: Two graphs which contain the same number of nodes connected in the same way are said to be isomorphic. 節點之間相互關係完全相同的兩個圖同構,即可以通過簡單的畫法調整得到彼此。
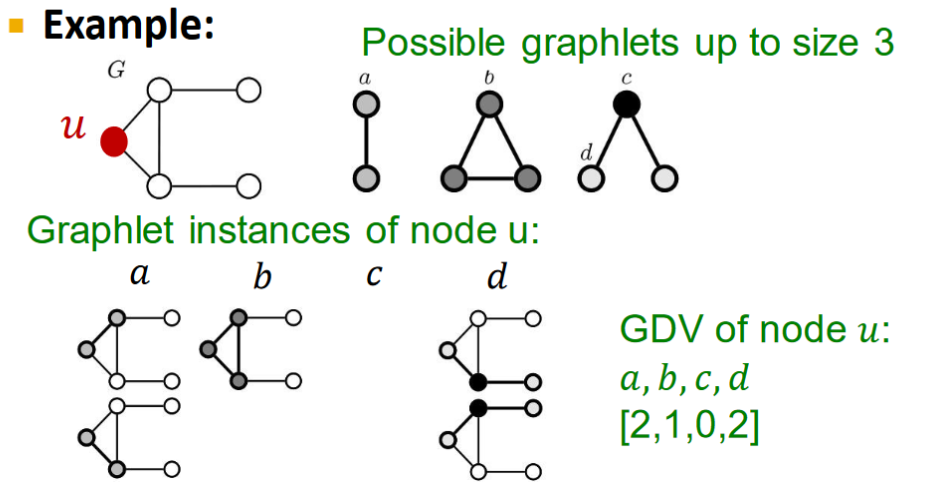
Graph Degree Vector(GDV): Graphlet-base features for nodes. GDV counts graphlets that a node touch. GDV表示某node參與的Graphlet數。
參考
- http://web.stanford.edu/class/cs224w/
- https://en.wikipedia.org/wiki/Graphlets
