Components of a Network(graph)
- Object: nodes,vertices
- Interactions: links,edges
- System: network,graph
Types of graph
- 有向圖與無向圖的選擇:
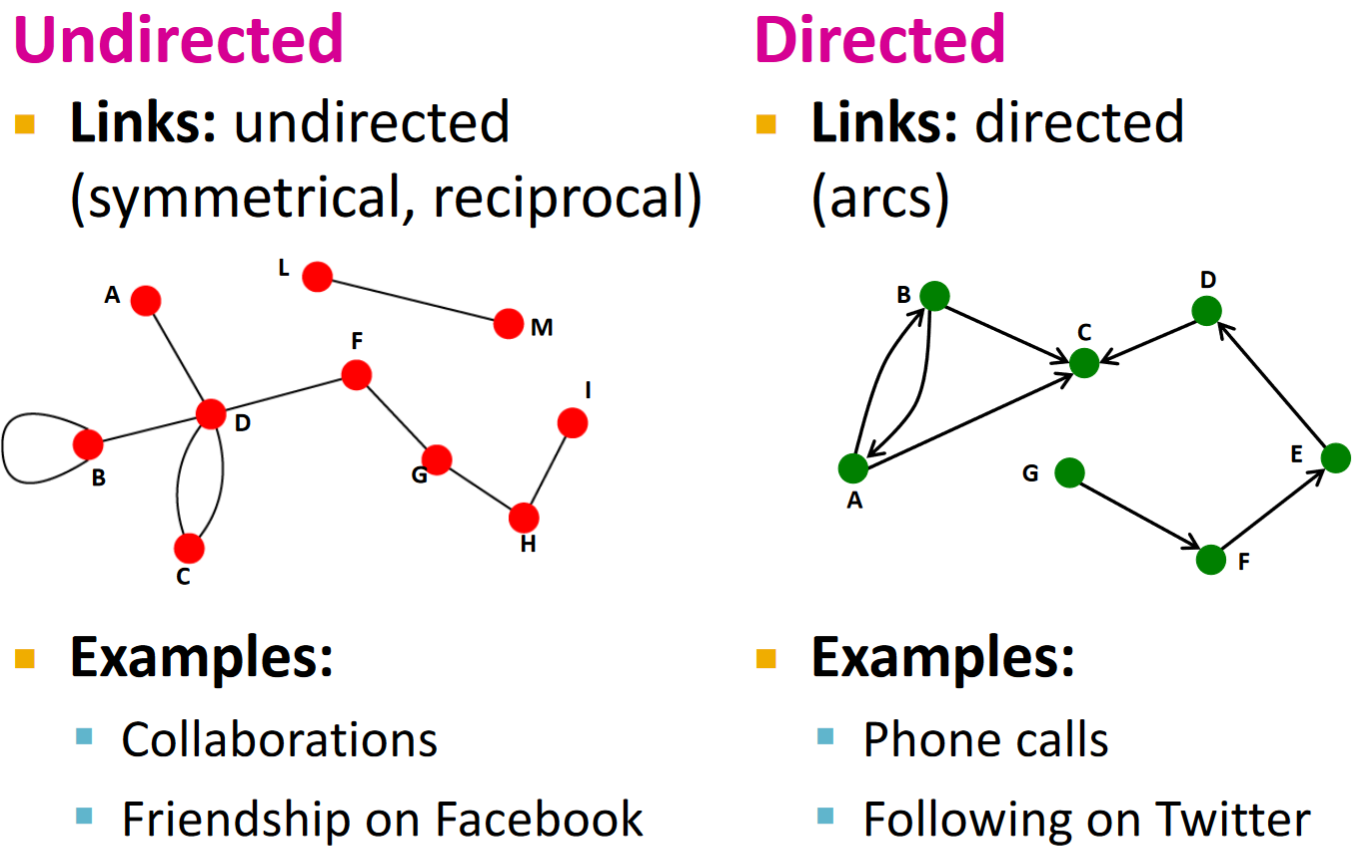
無向圖的節點間link表示一種對稱合作關係,有向圖則節點之間的relation有固定方向。
Node Degrees:
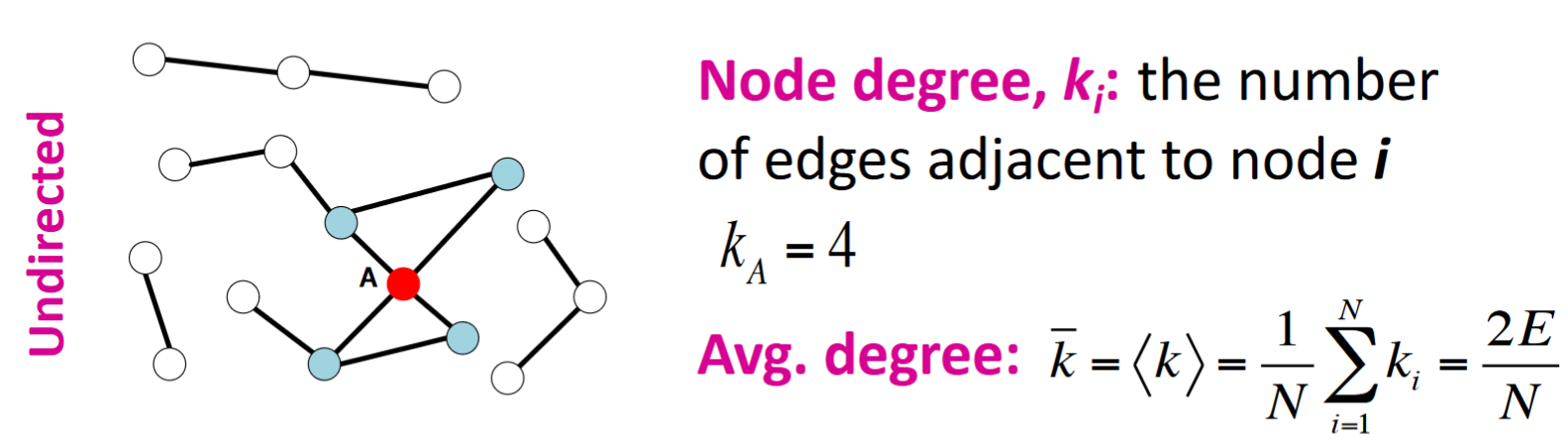
在無向圖中:Node degree表示某節點相鄰節點個數。平均node degree則可以直接用
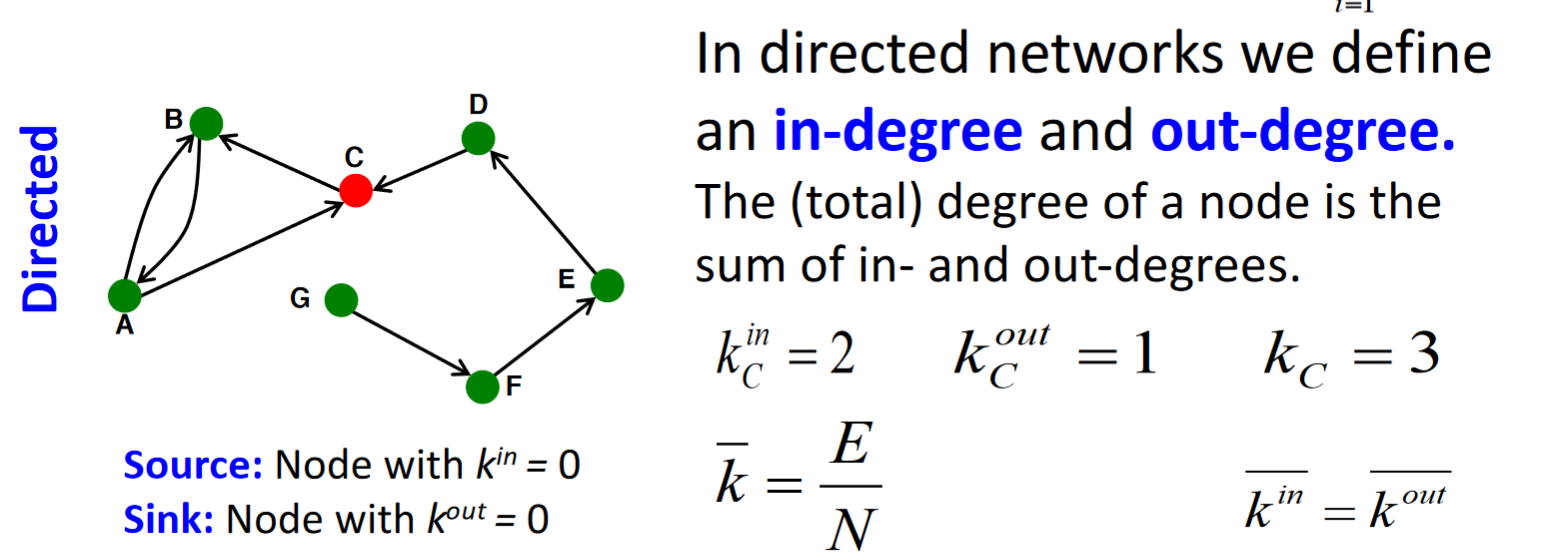
在有向圖中:定義了in-degree和out-degree, degree為in和out的sum。平均node degree則可以直接用
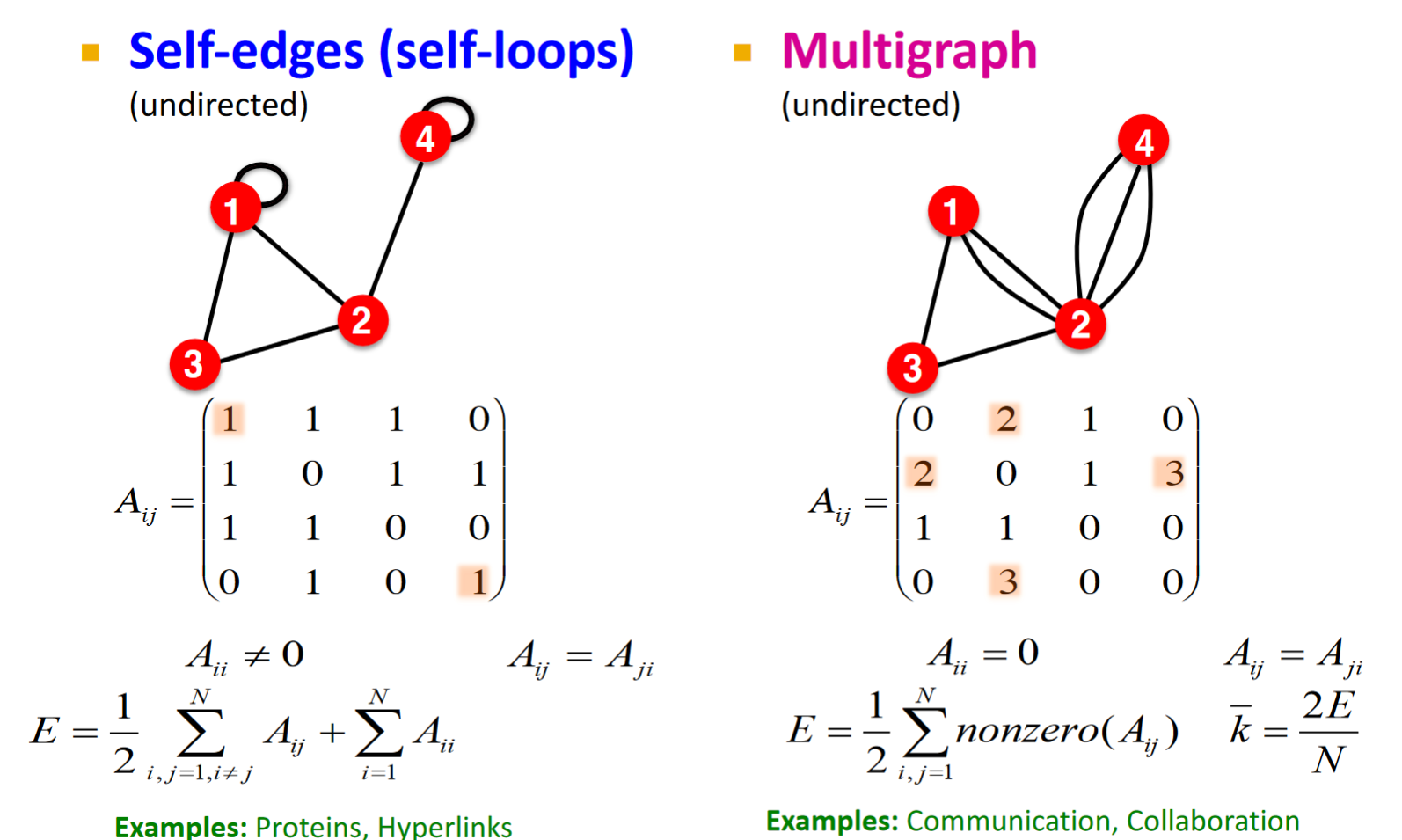
- Self-loops graph & Multigraph
含有self-loop節點的graph和節點之間有多link的graph,及其相應鄰接矩陣。
注意:self-loop節點的degree要加2因為自己連到自己算多兩個degree
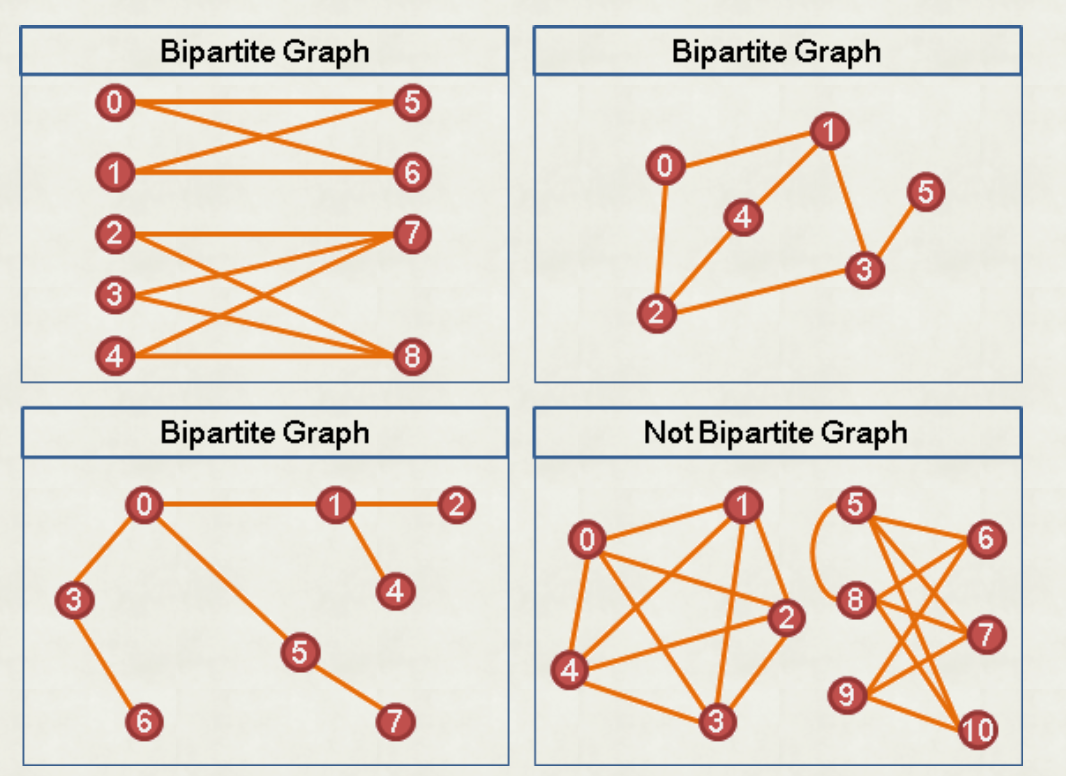
- Bipartite Graph(二部圖)
def:
Bipartite graph is a graph whose node can be divided into two disjoint set
and such that every link connects a node in to one in ; that is, and are independent sets.圖兩邊節點互相連通,而自身節點之間不連通。如論文發表者與其發表論文之間的關係可以用二部圖表示。
Folded/projected Bipartite Graphs
Projection U由對於連接在同一Vnode的Unode得到,Projection V反之同理。 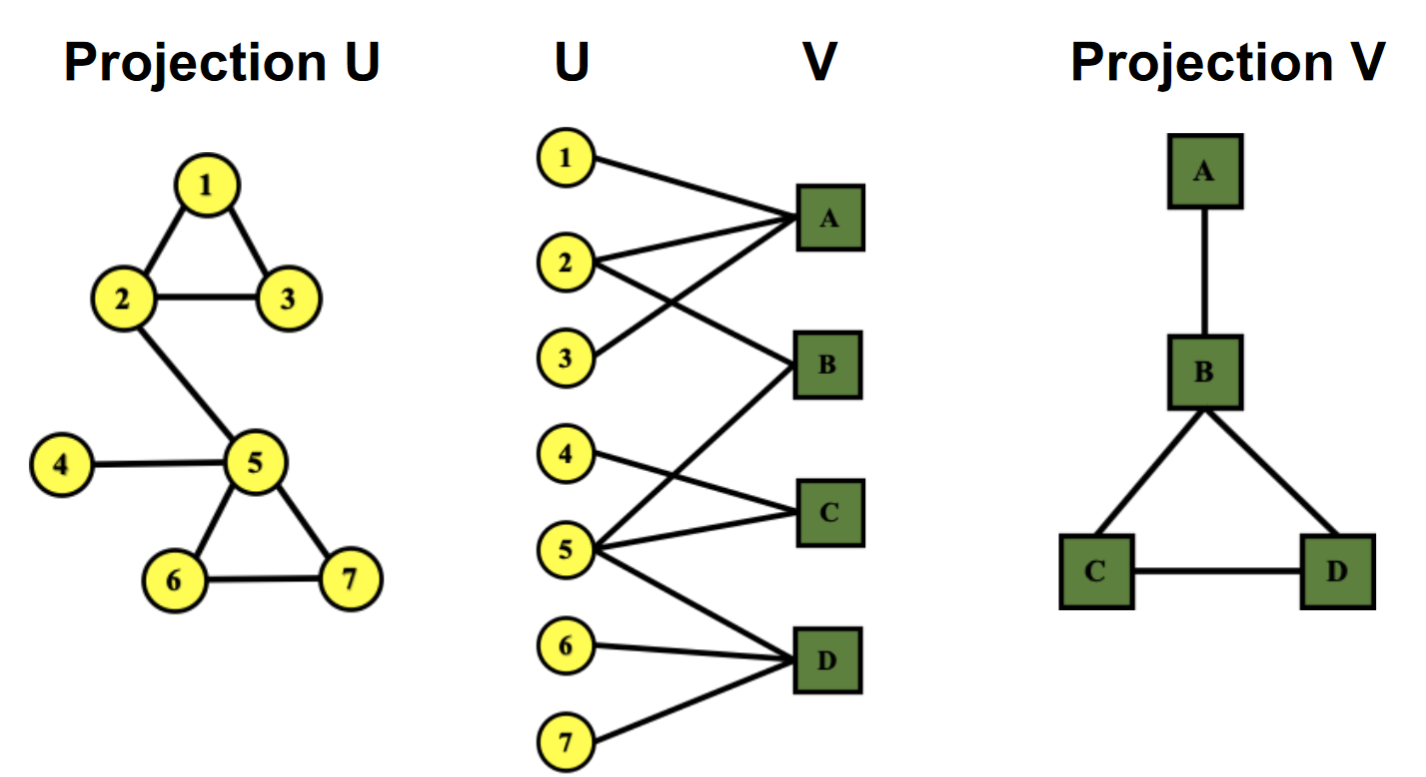
Representation of graph
- Adjacency Matrix(鄰接矩陣):
以矩陣內element的column,row表示對應graph上node之間的連通性(可能包含方向)。無向圖鄰接矩陣對某row或column做和可以得到相應node之degree。有向圖同理。
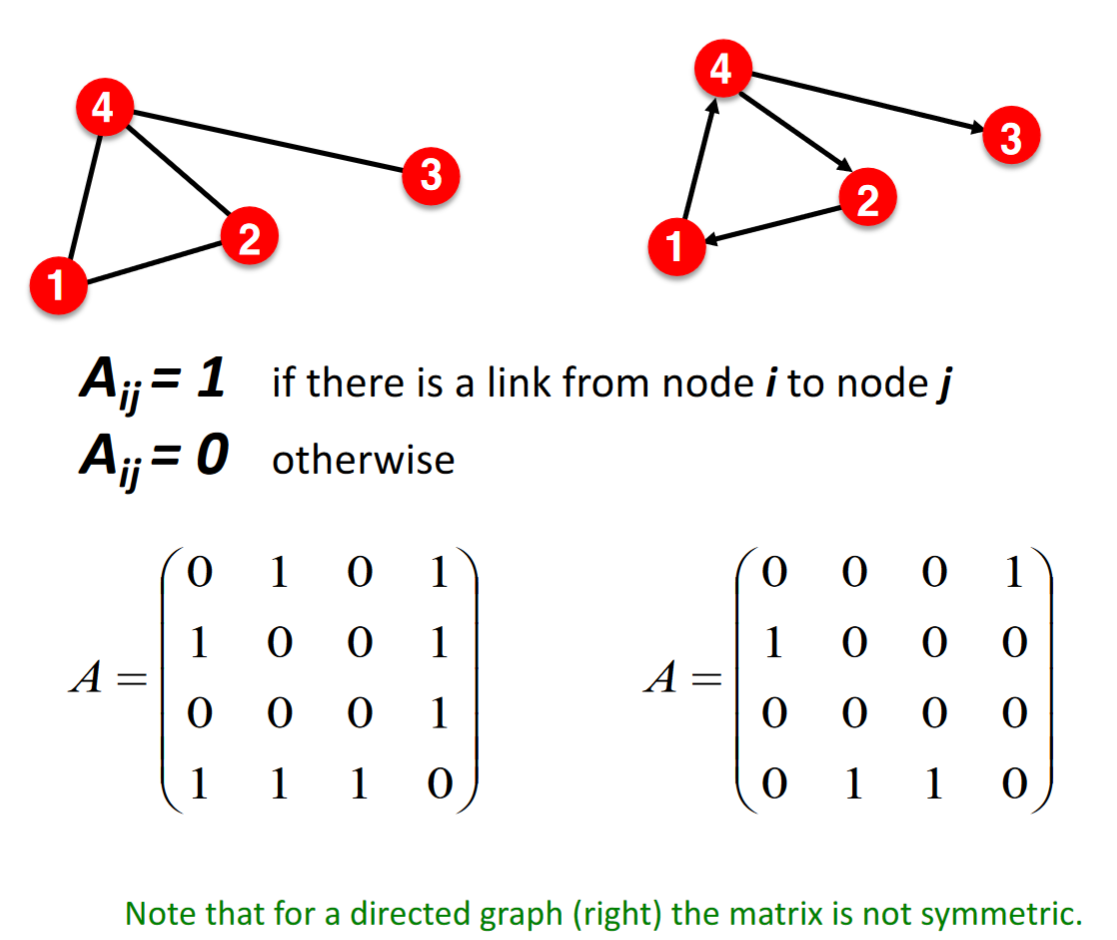
帶權重的graph對應鄰接矩陣:
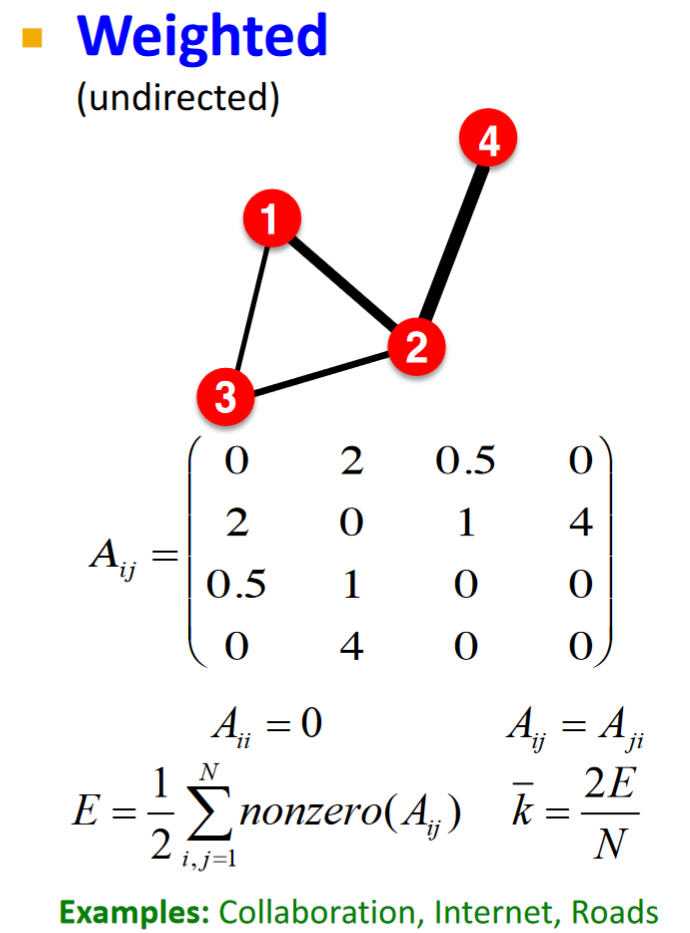
現實世界中形成的graph往往是sparse(稀疏的),相應鄰接矩陣內有許多element為0。
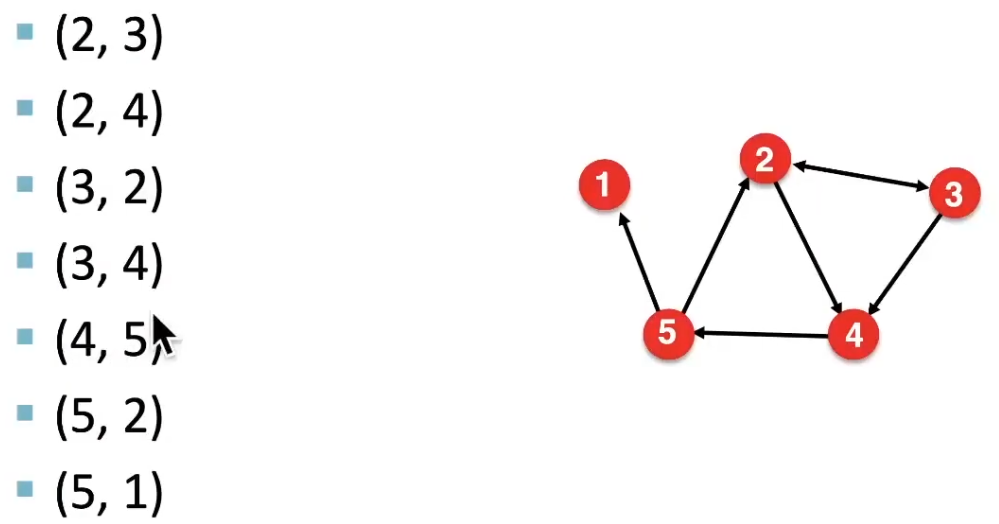
- Edge list
這種圖的表達形式缺點在於難以做 graph manipulation和graph analysis
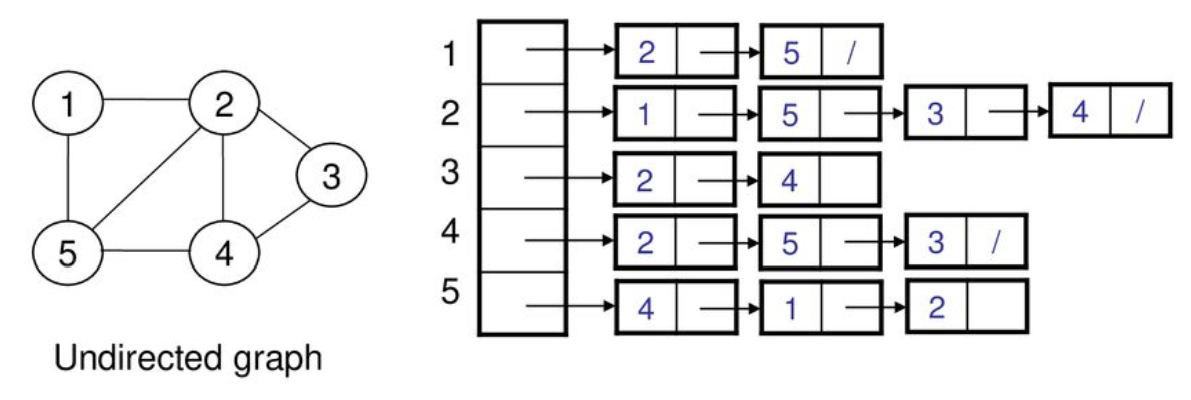
- Adjacency list
AL適用於garph非常大且稀疏的情況
Node and Edge Attributes
- Weight(edge權重)
- Ranking(LA概念)
- Type(節點類型)
- Sign(含正負屬性的edge)
- 依據不同應用設計的相應屬性
Connectivity of Graphs
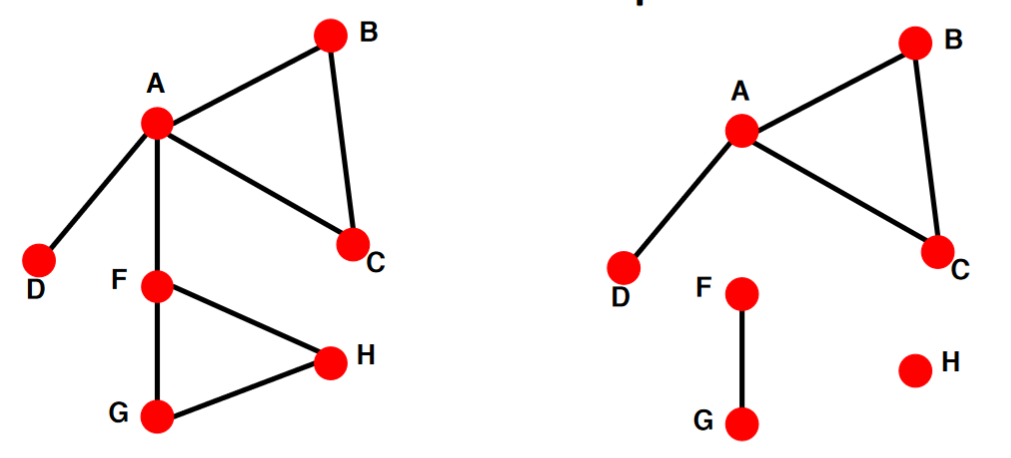
- Undirected Graph
任意兩個節點都要能連通(可以通過其他節點為中介),下圖左側為連通圖右側不是
- Directed Graph
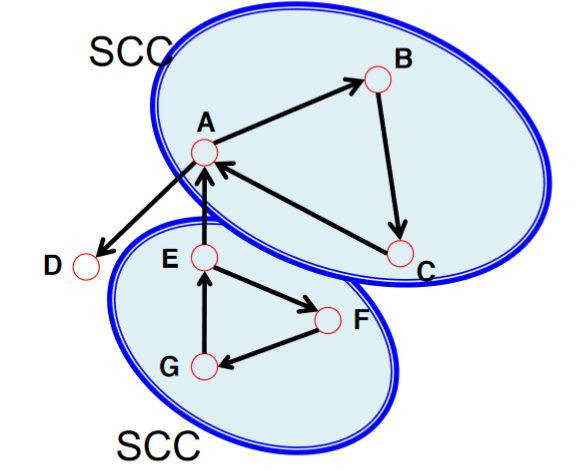
Strongly Connected: has a path from each node to every other node and vice versa 所有節點都必須能雙向互相連通
Weakly connected directed graph: is connected if we disregard the edge directions. 在不考慮edge方向的情況下可連通的有向圖。
Strongly connected component(SCC): graph中可構成強連接的sub-graph。
參考
- http://web.ntnu.edu.tw/~algo/
- http://web.stanford.edu/class/cs224w/
- https://slideplayer.com/slide/14678535/
