前言

之前討論的都是離散型的分布，意即隨機變數的取值是可數的。而本章討論取值不可數的連續情況。

連續隨機變數的機率密度函數和累積分布函數

類似於離散型隨機變數的機率質量函數(PMF),連續隨機變數有相似概念的機率密度函數(PDF):

對於累積分布函數,存在滿足：

那麼X為連續隨機變數，其PDF為。

連續隨機變數的期望值與變異數

期望值：

類似於離散型隨機變數的期望值如下：

我們可以得到連續型隨機變數的變異數如下：

變異數：

變異數與離散情況下定義相同:

和離散下相同，連續條件下也滿足:

均匀分布

對於一個在區間上均匀分配的隨機變數x，有:

圖像:

PDF:

CDF:

這邊CDF直接用長方形面積考慮可以得到:

期望值:

變異數：

常態分布(正態分布)

圖像:

常態分布的數學期望值或期望值 等於位置母數，決定了分布的位置；其變異數 的開平方或標準差 等於尺度母數，決定了分布的幅度。

PDF:

CDF:

一般討論標準常態分布的CDF:

with

數學期望:

let

is an odd function

變異數：

let

the middle one is an odd fuction

指數分布

圖像:

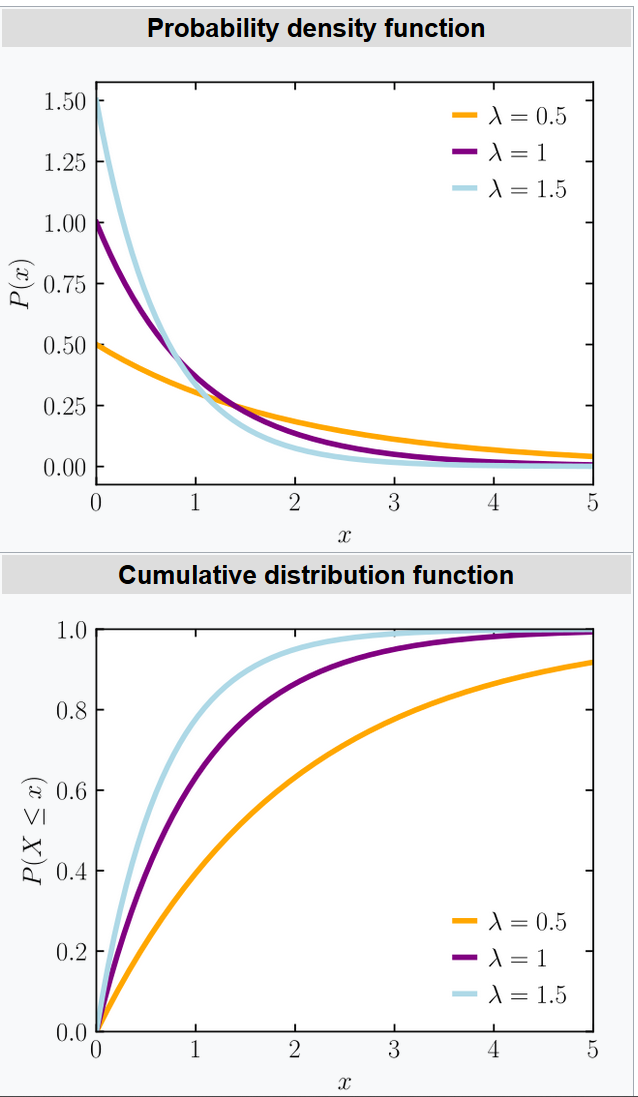
PDF:

CDF:

參考

  • Wikipedia