Linear Transformation(線性轉移)

Def:

let V and W be vector space(over F). A function T: V -> W is called a linear transformation from V to W if for all x,y ∈ V and C ∈ F such that:

<a> T(x+y) = T(x) + T(y)

<b> T(cx) = c*T(x)

Properties:

  1. if T: V -> W is linear then T(0) = 0

  2. T(ax + by) = aT(x) + bT(y)

  3. xi為基底向量時，實現了由基底向量轉移完成原向量的轉移

    Proof of 1 ：

    T(0) = T(0+0) = T(0) + T(0) = T(0*0) + T(0*0) = 0*T(0) + 0*T(0) = 0

    Proof of 2 ：

    T(ax+by) = T(ax) + T(by) = aT(x) + bT(y)

    Proof of 3 ： > 與2同理

兩種特殊轉移（單位轉移與零轉移）

  • Zero transformation(零轉移)

    Let T: R^n -> R^m be a function defined by T0(x) = 0, ∀ x ∈ R^n, then T0 is called the zero transformation from R^n to R^m.

    零轉移必為線性轉移，因為必滿足線性轉移的兩個條件。

  • Identity function(transformation) 單位轉移

    Let I: V -> V be a function defined by I(x) = x, ∀ x ∈ V, then I is called the identity function(transformation), which is a linear transformation.

以矩陣乘法表示線性轉移

Let A be an m-by-n matrix, for any x∈ R^n, matrix multiplication (A · X) is a transformation from R^n -> R^m, which is a linear transformation.

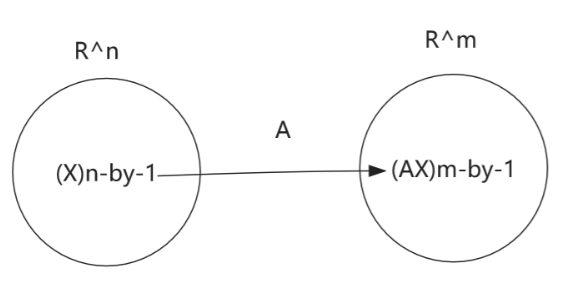
∀ A is an m-by-n matrix, then let TA: R^n -> R^m, defined by TA(x) = AX, ∀ x∈ R^n, which is a linear transformation from R^n to R^m

Here A is called the standard matrix for TA and TA is called the multiplication by A. [TA] = A

(重要)Theorem:

Let T: R^n -> R^m be linear and β = {e1 , e2 , ..., en} be the standard basis(標準基) for R^n, then there exists an m-by-n matrix A such that T(x) = A·X, ∀ x∈ R^n, where A = [T(e1) T(e2) ... T(en)]

Proof:

∀ x∈ R^n => x = [x1,x2,...,xn] = x1e1 + x2e2 + ... + xnen, xj ∈ R, 1 <= j <= n

T(x) = T(x1e1 + x2e2 + ... + xnen) = x1*T(e1) + x2*T(e2) + xn*T(en) --------(1)

∵ T(ej) ∈ R^m, 1<=j<=n

∴ Let T(ej) = [a1j,a2j,...,amj], 1<=j<=n --------(2)

Substitute (2) to (1)

where A = [T(e1) T(e2) ... T(en))]

證明思路：證明線性轉移可以用矩陣乘法表達。將解集向量X用標準基表達後依據線性特性的到T(x)為式1，再構造標準基形式使其貼合之後m-by-n矩陣的形式，最後代入整理為矩陣乘法的形式而得證。