Random Variable(隨機變數)
定義：
給定樣本空間(S,F)，如果其上的實值函數X:S->R 是 F(實值)可測函數，則稱X為（實值）隨機變數。
隨機變數是一種關於樣本空間的函數 
Cumulative Distribution Function(累積分佈函數)
機率累加結果的函數，機率質量函數的積分（連續），累加（離散）結果。
Probability mass function（機率質量函數）
在機率論中，機率質量函數（probability mass function，簡寫作pmf）是離散隨機變數在各特定取值上的機率。
離散條件下隨即變數某取值的機率
對於離散條件下顯然有（樣本空間內所有事件的機率和為1）：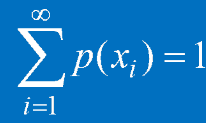 
Binomial distribution（二項分布）
在機率論和統計學中，二項式分布（英語：Binomial distribution）是n個獨立的是/非試驗中成功的次數的離散機率分布，其中每次試驗的成功機率為p。
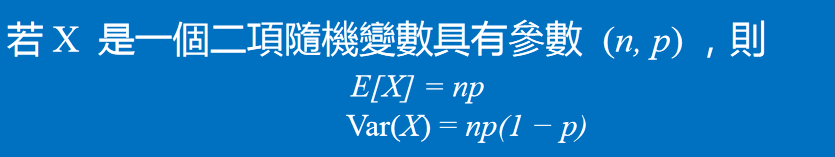
二項分布隨機變數取值遞推關係(連續兩項做比值推導而得)：
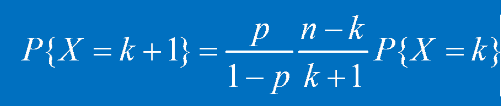
Bernoulli distribution(伯努利分布)
伯努利分布是二項分布的一種特殊情況（僅進行一次trail）
Poisson distribution(泊松分布)
泊松分布可視為二項分布中n足夠大且λ=np適中時的一種近似計算。在泊松分布機率質量函數推導過程中有： 
機率質量函數: 
數學期望：
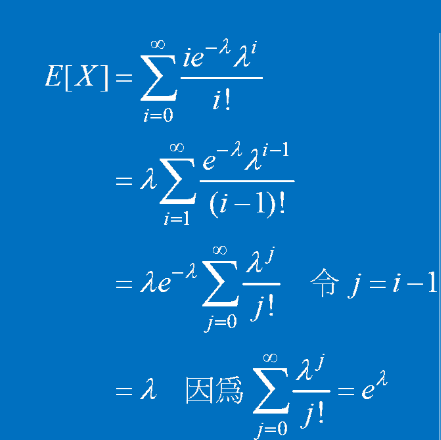
變異數：
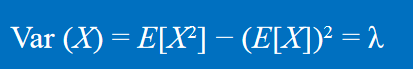
泊松分布的期望和變異數都可以由二項分布在n趨於正無窮和p趨於0的情況下直接得到。 期望：E(X) = np = λ 變異數：np（1-p）with p趨於0 = λ（1）= λ
遞推公式：
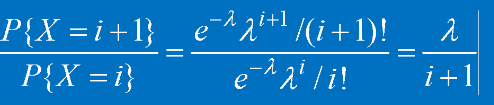
幾何分布
一種特殊的二項分佈(僅最後一次成功)
幾何隨機變數的期望：
幾何隨機變數的變異數：
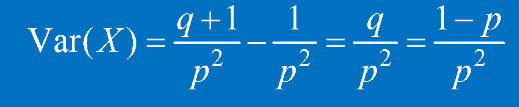
Negative binomial distribution(負二項隨機分布)
負二項式分布（Negative binomial distribution）是統計學上一種描述在一系列獨立同分布的伯努利試驗中，成功次數到達指定次數（記為r）時失敗次數的離散機率分布。
機率質量函數:
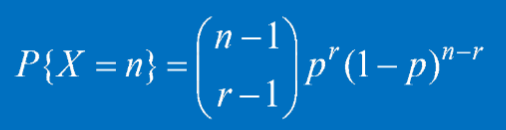
其中r為累積的成功數，n為trail的總次數。來源為：因為正好累積了r次成功，所以最後一次必為成功，那麼從前n-1次trail中選擇r-1次為成功情況，得到該機率質量函數。
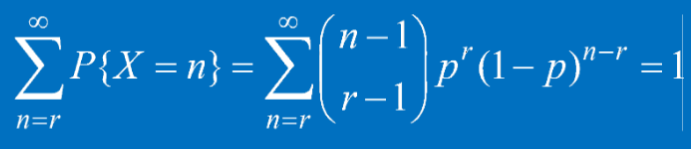
注意：
參數為(r,p)的負二項分布期望、變異數推導： 
為方便變異數推導，推廣上式為：
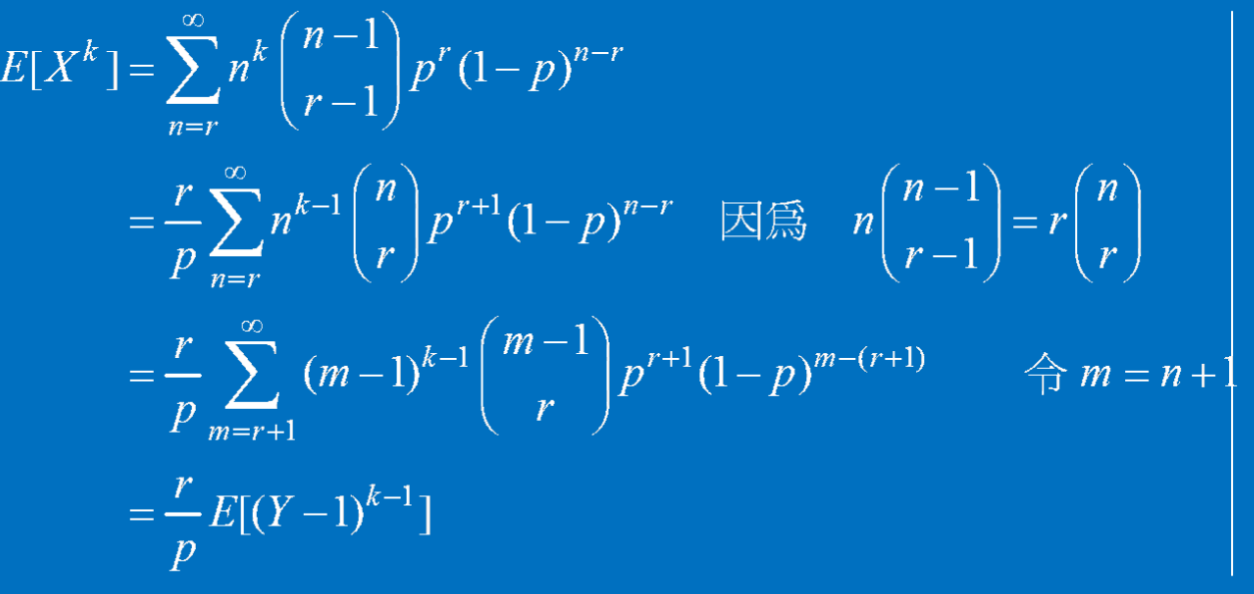
注意：Y是有參數(r+1,p)的負二項隨機變數
帶入k=1&k=2計算變異數：
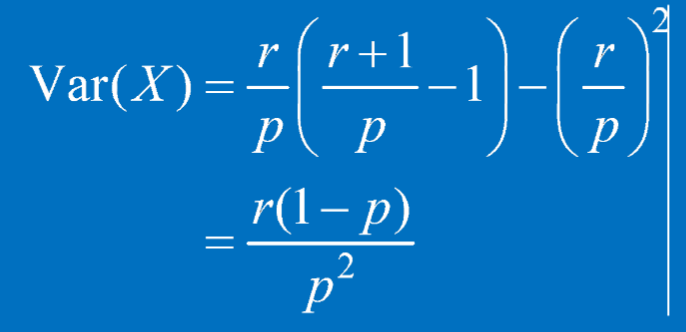
Hypergeometric distribution（超幾何分布）
超幾何分布（Hypergeometric distribution）是統計學上一種離散機率分布。它描述了由有限個物件中抽出n個物件，成功抽出指定種類的物件的個數（抽出不放回 （without replacement））。
PMF of Hypergeometric distribution:
總數為N，抽取數為n，抽取到的特殊種類物件數為i，特殊物件總數為m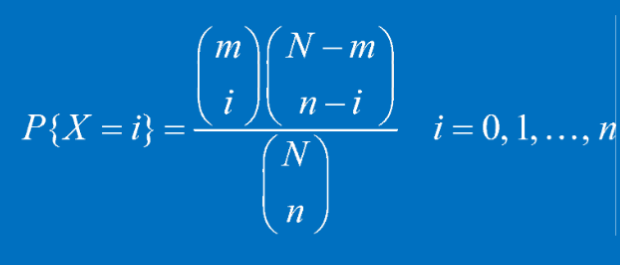 
超幾何分布的期望值和變異數：
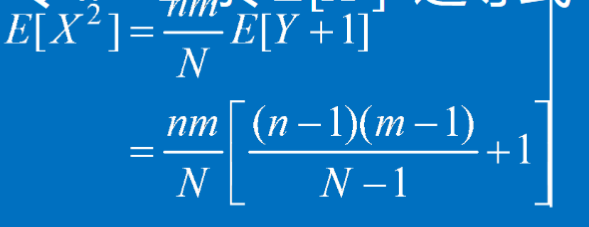
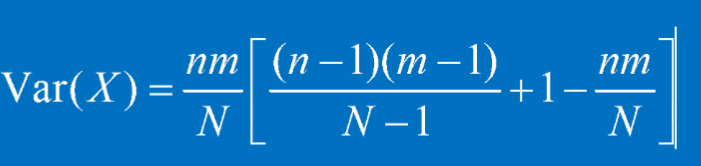
Expected value(期望值）
隨即變數有限取值下定義：
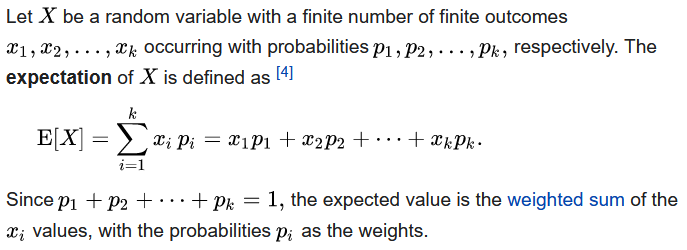
期望即為對隨機變數值的加權平均（以各隨機變數值對應機率為權重）
某隨機變數的線性函數期望值滿足(隨機變數的線性函數期望值等於隨機變數的變異數乘以係數加上常數)： 
隨機變數和的期望等於他們期望的和:
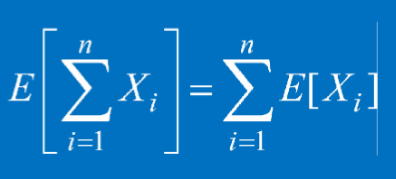
Variance（變異數、方差）
變異數，應用數學裡的專有名詞。在機率論和統計學中，一個隨機變數的變異數描述的是它的離散程度，也就是該變數離其期望值的距離。
有(變異數為平方的期望減去期望的平方):
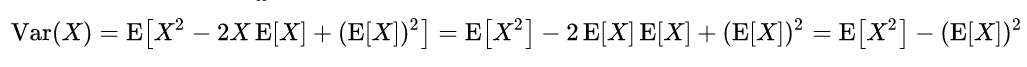
對於隨機變數的線性函數的變異數有(隨機變數的線性函數的變異數等於隨機變數變異數乘以係數的平方)：
對變異數開平方根叫做標準差: 
一些題目
這邊要特別注意：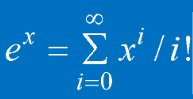 
該式可以將c用λ代換，減少參數。
泊松分布用來進行某時間段內事件發生預測時，預測幾個時間段即相應的λ要變為幾倍。
總結
分布 機率質量函數 期望 變異數 二項分布 Cn,k*pk(1-p){n-k} np np(1-p) 伯努利分布 q,for k=0;p,for k=1 p p(1-p) 泊松分布 e^(-λ)*λ^i/i! λ λ 幾何分布 (1-p)^(k-1)*p 1/p (1-p)/p^2 負二項分布 Ci-1,r-1 * P^r * (1-p)^{i-r} r/p r(1-p)/p^2 超幾何分布 Cm,i * C(N-m),(n-i)/CN,n i=0,1,...,m nm/N & - 真夠累的，生日看得我頭暈腦脹@@
參考
- Wikipedia
- https://zhuanlan.zhihu.com/p/166653762