Theorem: 倘若方陣有一row或一column全為0,則該方陣的行列式為0
Let A be a square matrix , if A has a row of zeros or a column of zeros, then det(A) = 0
對全是0的row或column使用cofactor expansion(降階法)可明顯得到。
Theorem: 方陣的行列式等於其轉置矩陣的行列式
let A be a square matrix,then det(A) = det(A^T)
轉置後原來的row變為column,對其進行降階可明顯得到。
Theorem: 做ERO時矩陣行列式的變化

該theorem可以用於在計算複雜矩陣的行列時時對矩陣進行簡化後用簡化矩陣的行列式倒推原矩陣行列式(在row或column湊出儘量多的0或1方便降階運算)
如:

Theorem: 用基本矩陣表示做ERO時矩陣行列式的變化
Let E be an n-by-n elementary matrix, then
det(E (multiply row by non-zero scalar k) ) = k, k≠0
det(E (interchange two rows) ) = -1
det(E (adding a scalar multiple of one row to another) ) = 1
Vandermonde matrix(范德蒙矩陣)
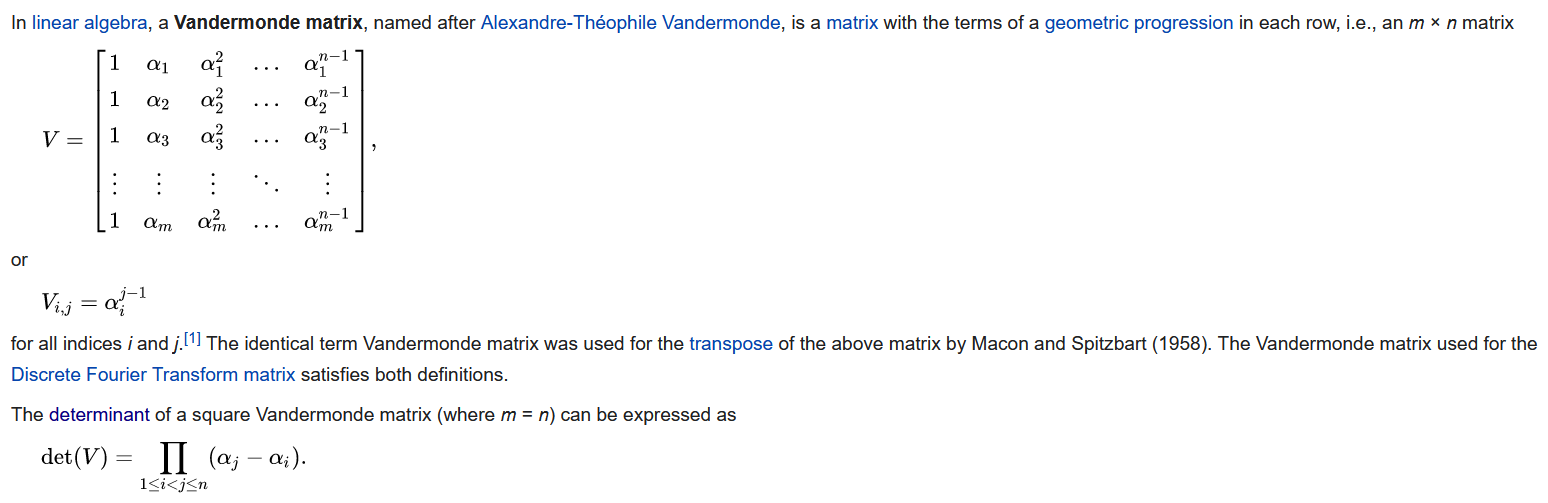
范德蒙矩陣的行列式計算只要關注第2個column,或者其轉置矩陣的第二個row。
范德蒙矩陣行列式計算如例:

參考資料
- University of waterloo math 106: https://my.cel.uwaterloo.ca/p/form/courses/search/course/sub/MATH/cat/106/topic/0
- Wikipedia :https://en.wikipedia.org/wiki/Vandermonde_matrix
- https://www.superprof.co.uk/resources/academic/maths/linear-algebra/determinants/vandermonde-determinant.html
