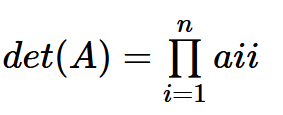Determinant(行列式)
低階數矩陣的行列式計算
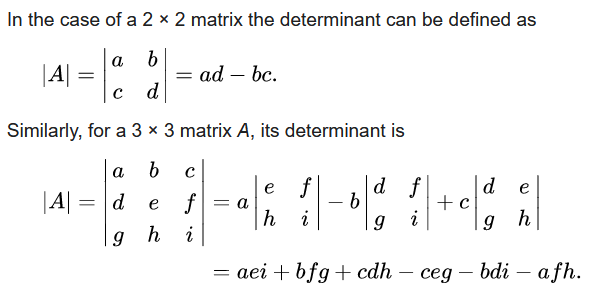
這邊三階行列式公式用降階的方法得到。
Minor and Cofactor
if A is a square matrix, then the minor(子式) of entry aij, denoted by Mij, is defined to be the determinant of the submatrix that remains after the ith row and jth column are deleted from A. The number (-1)^(i+j) Mij, denoted by Cij is called the cofactor(餘子式) of entry aij.
minor(子式)是刪除某行列後的行列式值,是一個數值。對應的cofactor(餘子式)也是一個數值。 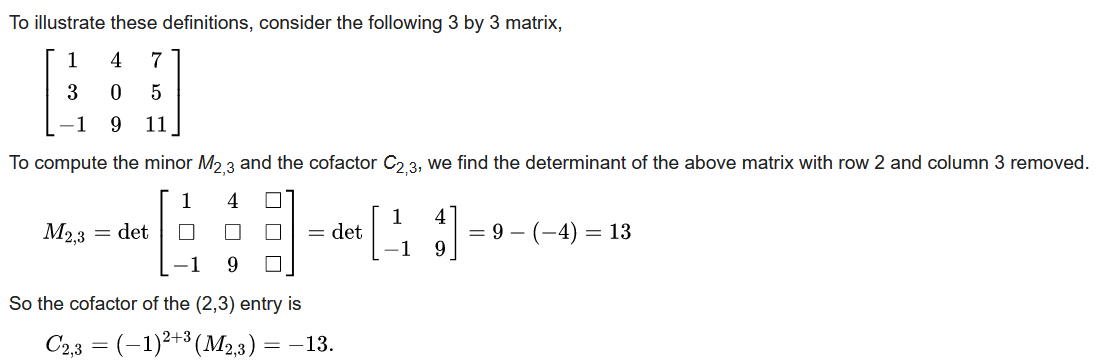
cij = (-1)^(i+j) Mij
Theorem:方陣任意row或column的所有項與項的餘子式乘積之和相等,且該乘積即為矩陣的行列式值。
if A is an n-by-n matrix, then regardless of which row or column of A is chosen, the number obtained by multiplying the entries in that row or column by the corresponding cofactors and adding the resulting products is always the same.
即對於矩陣A有:
det(A) = ai1·ci1 + ai2·ci2 + ... + ain-1·cin-1 + ain·cin i∈[1,n]
= a1j·c1j + a2j·c2j + ... + an-1j·cn-1j + anj·cnj j∈[1,n]
該方法可以應用於行列式計算時的降階法(因為) cofactor對應minor,而minor會刪掉某row與column。如下例子:
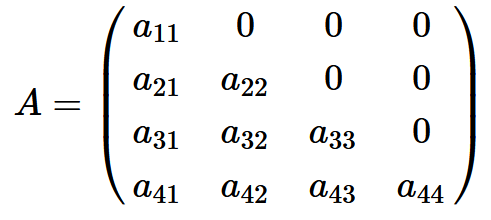
我們對於row1進行降階。有:
det(A)
= a11·c11 + 0·c12 + 0·c13 + 0·c14
= a11·c11 = a11 · (-1)^(1+1) M11
= a11 |a22 0 0 , 0 a33 0 , 0 0 a44| (再對第一row降階)
= a11 · a22 · c22
= a11 · a22 · (-1)^2 |a33 0, 0 a44|
= a11 · a22 · a33 · a44
該結果也印證了三角形矩陣的行列式值為主軸乘積。
Theorem:三角形矩陣的行列式值為主軸乘積
If A is an n-by-n matrix then
參考
- Wikipedia