Conditional Probability(條件機率)
Def:
In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event has already occurred.
條件機率指的是某事件已經發生的條件下,另一事件發生的機率。
B條件下A發生的機率記為:P(A|B)
有下式成立:

亦有下式成立:

在機率運算中可推得: 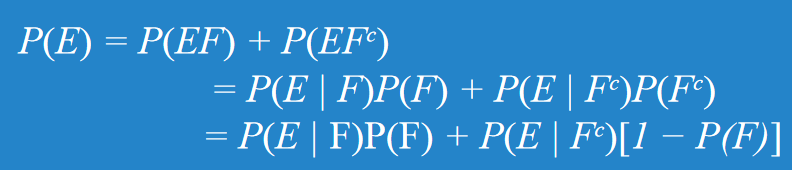
該式說明在計算某事件機率時,可以由該事件的某條件事件及其餘事件得到。
貝氏法則:

可簡單由上式推導得到。
貝氏法則可以得到條件與事後事件互換事件的機率。
互相獨立事件

注意:互相獨立事件和互斥事件是兩個不同的概念。如擲一枚硬幣,結果正反互斥,而與再擲一枚這一事件互相獨立。
互相獨立事件結合貝氏法則我們可以得到:
P(B|A) = P(B)
因為事件A與B互相獨立,所以A這一條件并不影響之後的B的機率,所以該等式成立。
互相獨立事件與對方的餘事件亦互相獨立
If A and B are independent, then A and B^c(complement event of B) are independent.
若事件A與B互相獨立,則A與B的餘事件也互相獨立。
三個事件互相獨立的條件

條件獨立(條件機率與互相獨立事件的結合)

有點意思的題目
卡片顔色問題

這題目直接用貝氏定理展開計算并不難,但有意思的在於倘若你直接讀題思考,容易陷入:朝上一面是紅色,可能性只剩下紅紅和紅黑兩張牌,所以答案為1/2的誤區。而實際上朝上的一面為紅色有三種可能,因為紅色牌的兩面都可能朝上,所以答案為1/3。
費馬
進行一串獨立試行,其成功的機率為p,失敗的機率為1 − p。求在m次失敗前出現n次成功的機率。
解:
Fermat的論點是:m 次失敗前出現n次成功的充要條件是在首m+n−1 次試行中至少有n次成功 。
所以答案為:
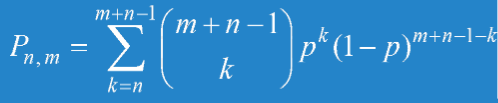
參考資料
- Wikipedia
