前言
本篇關於可逆矩陣和一些矩陣運算的特點補充。
Properties of matrix arithmetic
這部分在第一篇已經講述過。但特別注意以下:
- proof of A·(B+C) = A·B + A·C :
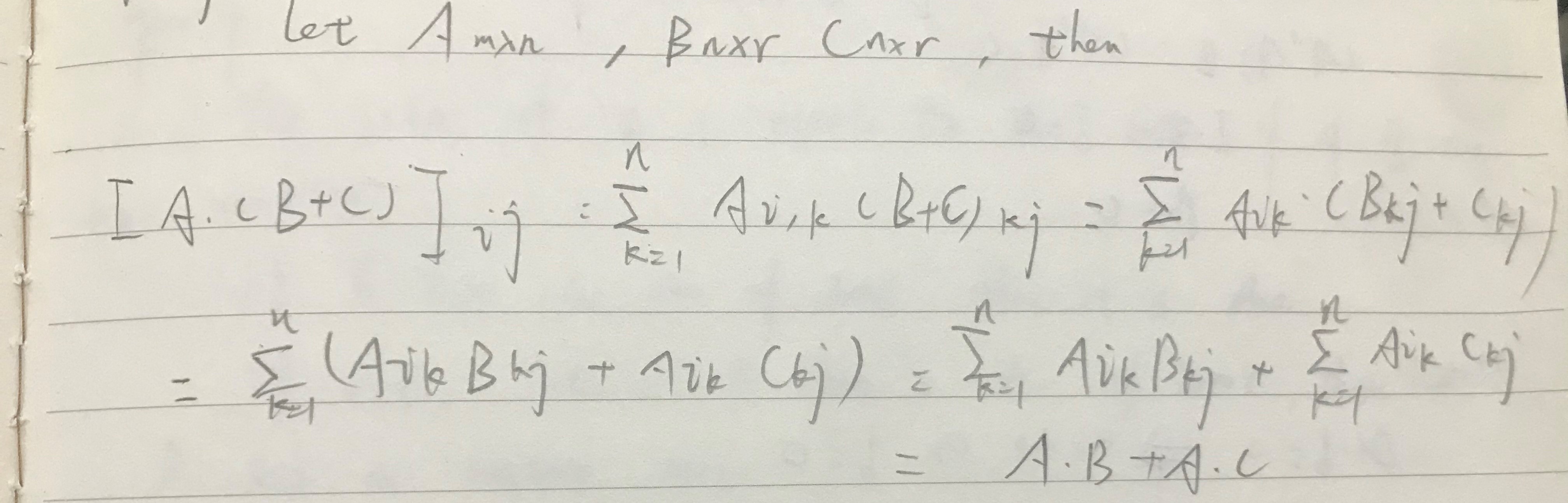
證明思路:通過矩陣乘法公式展開後,通過純量的分配率構建出矩陣乘法的分配率。
什麽條件下 A·B = A·C => B=C
- A is invertible(A可逆),等同於 det(A) != 0
- the operator is associative 運算符要滿足結合律
以上兩點滿足則: > AB = AC > > A^-1 (AB) = A^-1 (AC) ---需存在逆矩陣 > >(A^-1 A)B = (A^-1 A)C ---需運算符滿足結合律 > >B = C
A·B = 0 ≠> A=0 or B =0
Identity matrix(單位矩陣)
A square matrix with 1 on the main diagonal and zeros elsewhere is called a identity matrix:
(重要)方陣的RREF特性
if R is the reduced row echelon form of an n-by-n matrix A, then either R has a row of zeros or R is the identity matrix In.
方陣的RREF要麽有一個row全為0,要麽為單位矩陣。(一個row為0對應該方陣不可逆,為單位矩陣則對應該方陣可逆。)
proof:
The size of R is equal to the size of A is an n-by-n matrix
if R has a row of zeros ,then proof is done
if not, i.e. R has no row of zeros ,then
R has n nonzero rows
=> R has n leading 1
=> every row and column has leading 1 ---因為R是方陣
=> Rij = Iij for all i,j
i.e. R is a identity matrix.
證明思路:因為要證明A OR B關係,所以假設A不成立下B一定成立則得證。R沒有全0row時必得到R每一row與每一column必都有leading1,所以R即為I
可逆矩陣與之逆矩陣(A and A^-1)
定義: > if A is a matrix, and if a matrix B can be found such that A·B = B·A = I, then A is said to be invertible(nonsingular) and B is called an inverse of A. If no such B can be found, then A is said to be singular(non-invertible)
注意隱含了A、B都是方陣,即可逆矩陣一定是方陣
注意:

等order(size)的方陣AB有AB = I則一定BA=I。即證明矩陣可逆時,從兩個中證明一個即可。
怎樣找到可逆矩陣的逆矩陣

同時對可逆矩陣A和同size的單位矩陣I做相同的ERO直到A變為單位矩陣(RREF of A),I變化後得到的矩陣即為A的逆矩陣A^-1
可逆矩陣之逆矩陣的唯一性
The inverse of an invertible matrix is unique.
proof:
suppose that both B and C are inverse matrices of an invertible matrix A then:
B = B I = B (A C) = (B A) C = I C = C
i.e. B = C
證明思路:假設某可逆矩陣有兩逆矩陣,推理得到他們相等,為同一矩陣。得證。
從行列式角度看矩陣是否可逆
The matrix A is invertible if and only if det(A) ≠ 0.
行列式為0的方陣不可逆。
可逆矩陣特性
可逆矩陣(方陣)的乘積的逆矩陣為反序各自逆矩陣的乘積
if A and B are invertible matrices of the same size then AB is invertible with (AB)^-1 = A^-1 · B^-1
推而廣之:
(AnAn-1...A2A1)^-1 = A1^-1 A2^-1 ... An-1^-1 An^-1
矩陣乘積可逆的充要條件
(AB) is invertible if and only if both A and B are invertible
矩陣A與B乘積矩陣AB可逆的充要條件是矩陣A和矩陣B皆可逆
proof:
(A·B) · (B-1·A-1) = A ·(B · B^-1) · A^-1 = A·I·A^-1 = A·A^-1 = I
and
(B-1·A-1)·(A·B) = B^-1 ·(A^-1·A)·B = B^-1 · I · B = B^-1 · B = I
依據可逆矩陣定義,則(AB)^-1 = (B-1·A-1)。
即當且僅當A與B皆可逆時,乘積矩陣AB可逆。
證明思路:以可逆矩陣定義結合矩陣乘法結合律找到AB的逆矩陣(B-1·A-1),進一步說明A與B都需可逆這一充要條件。
矩陣A可逆可導出的其相關矩陣特性
if A is invertible and n is a nonnetgative integer,then
<a> A^-1 is invertible and (A-1)-1 = A
<b> A^n is invertible and (An)-1 = A^-n
<c> k·A is invertible for any nonzero scalar k, and (k·A)^-1 = k^-1 · A^-1 可見純量的冪運算和矩陣的冪運算有可以合併之處
proof of <a>:
A^-1 · A = A · A^-1 = I
證明思路:第一個等號用A是可逆矩陣的特性得到特殊之交換律,後邊顯然得證。注意第一個等號兩邊不要交換順序,因為根據可逆矩陣的定義,這樣的書寫方式更加完備。
可逆矩陣結合轉置矩陣的特性
if A is an invertible matrix, then A^T is invertible and (AT)-1 = (A-1)T
若矩陣A可逆,則A的轉置矩陣AT可逆且AT的逆矩陣為A的逆矩陣的轉置矩陣。
Proof:
A^T · (A-1)T = (A^-1 · A)^T = I^T = I
(A-1)T · A^T = (A·A-1)T = I^T = I
i.e. (AT)-1 = (A-1)T
證明思路:用可逆矩陣的定義證明,注意合併轉置矩陣時要逆序。
