前言
此篇記録紀律統計CHAP2關於樣本空間和概率公設的內容。
樣本空間
樣本空間定義:
In probability theory, sample space (also called sample description space or possibility space) of an experiment or random trial is the set of all possible outcomes or results of that experiment. 一試驗所有可能結果的集合稱謂樣本空間,以S表示。
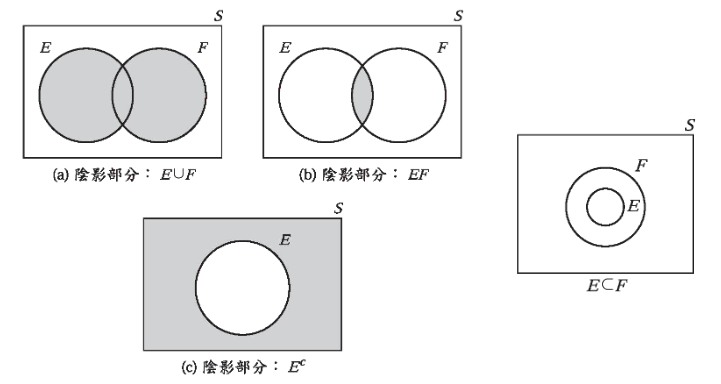
mutually exclusive events(互斥事件):
若P(A and B) = 0,則稱AB為互斥事件,即AB沒有交集。 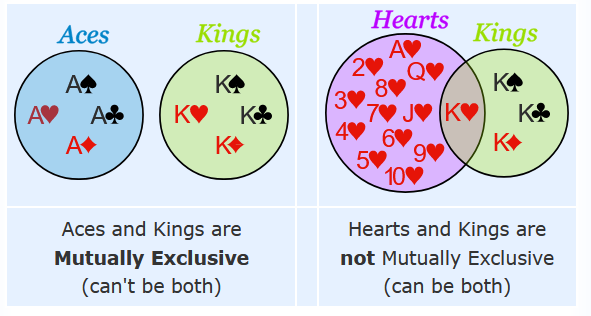
多事件聯集符號與多事件交集符號
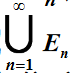
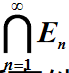
complement event符號:
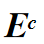
DeMorgan’s law
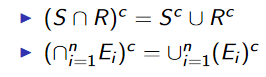
機率公設(Probability axioms)


Inclusion–exclusion principle(排容原理)

隱含了將聯集轉換為交集處理
排容原理在機率中應用:

例如(匹配問題):

首先題目求所有男人都拿到別的男人的帽子的概率,我們轉化為求1-P(至少一個男人拿到自己帽子的概率), 設Ei,i=1,2,3...,N表示第i人拿到自己帽子的事件,則依據排容原理有至少一人拿到自己帽子概率為(式一):
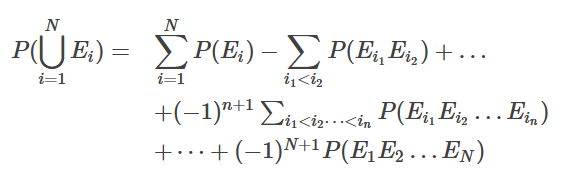
又從N人中挑出n人:Ei1,Ei2,...,Ein這n人都拿到自己帽子的概率為: 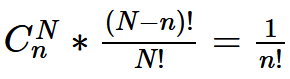
代換所以有式一即: 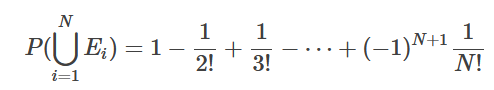
所以有P(沒有一個男人拿到自己帽子) = 1 - P(至少一個男人拿到自己帽子的概率)=
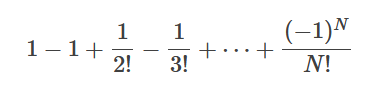
需注意的題目
連串問題:

首先考慮樣本空間總數為(multiset):(n+m)!/(n!*m!) 或者也可以等價考慮為(n+m)取n置n勝。
設: 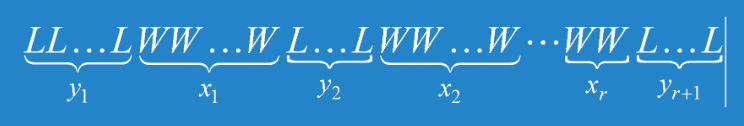
且令(因為首尾處可以不L,但這樣的話就不能配合後面求取方程正整數解,所以做如下代換完成關於y之方程變量特性的統一): 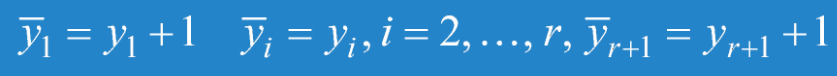
那麽題目轉化為求以下兩方程之正整數解數乘積除以樣本空間總數: 
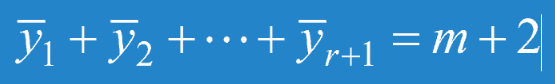
所以最終結果為:

習題1:

習題2:

計算某數的因數個數時,先將其以質數因式分解,然後結果為各質數之指數加一的乘積(意為不取該因數或取幾個該因數)。
參考
- WIKIPEDIA
- https://blog.csdn.net/pdcxs007/article/details/49364781
