前言
此篇是關於CHAP1:線性方程組與矩陣的筆記。
System of Linear Equations
相關定義
Def of equation:
A mathematical sentence with an equal sign (=) to indicate that two expressions name the same number
用等號表明其兩邊數學表達式數值相同的式子叫做等式
如:
x^3 + y^3 = 9 , 3x + 2y = 0, sinx + 2y = 0
Def of linear equation:
A linear equation in the n variable x1,x2,x3....,xn is defined to be one that can be expressed in the form a1x1+a2x2+a3x3+....+anxn = b, where a1,a2,...,an and b are constant.
如:
x - y + 3Z = 1
Note:
a1x1+a2x2+.....+anxn is called a homogeneous linear equation if b=0,otherwise,it's called nonhomogeneous. 常數項為0的線性方程稱為齊次線性方程,反之為非齊次。
A finite set of linear equations is called a system of linear equations or a linear system. The variables are called unknows. 有限的線性方程集合稱為線性方程組,其中變數稱為unknow。
線性方程組的表達方式:
- general form

- matrix eqution

where A is called the coefficient matrix(係數矩陣), X is called the solution vector, b is called the constant vector.
Def of Augmented matrix(增廣矩陣) of the linear system:

如:

當僅僅constant vecotr(b)不同時,可以簡單的表示幾個增廣矩陣為:
AX=b, with b=b1,b2,b3 表示為:[A|b1|b2|b3] ->(ERO) [A'|b1'|b2'|b3']
Gauss–Jordan elimination(高斯約當消去法)

由高斯消去法(forward pass)得到REF,再經由約旦的方法(backward pass)消去leading1所在column得到RREF,由RREF即可得到general solution.
Types of Elementary row operations:

- row交換操作:矩陣中互換兩個row位置
- row乘法操作:矩陣某一row中每一個元素同時乘以某非0常數
- row加法操作:矩陣中某一row可被本row和其他row的倍數和替代
Elementary row operations合理性驗證:
- 交換操作:互相兩row條件之間為and關係,而and關係滿足交換律,故可以交換
- 乘法操作:元素同時擴大不影響解集(Solution set k = solution set k'),而當同乘0時原線性方程組的解集將變化(Solution set k != solution set k')
- 加法操作:即帶入消元法應用
Gaussian elimination, also known as row reduction, is an algorithm in linear algebra for solving a system of linear equations.
Def of Row echelon form(階梯型矩陣):
- Any row consisting entirely of zeros occurs at the bottom of the matrix.全是0的row置於底部
- For each row that does not contain entirely zeros, the first non-zero entry is 1 (called a leading 1).每一個非全0row的第一個非0項是1,這個項叫做leading 1
- For two successive (non-zero) rows, the leading 1 in the higher row is further left than the leading one in the lower row. 對於兩個連續的非全0row,上邊row的leading 1較下邊row於更左邊。
some facts of about REF: * REF of A are not unique * RREF of A is unique * The leading 1 always occur in the same positions in A, those are called the pivot(樞紐) position of A. * Pivot column: a column of A that has leading 1 * Pivot row: a row of A that has leading 1 * A nonzero entry in a pivot position of A is called a pivot of A
例子: Find (1)pivot rows (2)pivot columns (3)pivots of A where: 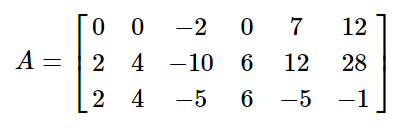
通過ERO獲得REF:

所以: (1):pivot rows:1,2,3 (2):pivot columns:1,3,5 (3):pivots of A: -10,-5
Def of Reduced row echelon form >* 滿足REF的定義 >* each column that contains a leading 1 has zeros everywhere else in this column. 含有leading 1的column其餘項皆為0
Steps for Gauss-Jordan Elimination:
- Swap the rows so that all rows with all zero entries are on the bottom. 將全是0的row置於底部
- Swap the rows so that the row with the largest, leftmost nonzero entry is on top. 將左端第一個非0項最大的row置於頂部
- Multiply the top row by a scalar so that top row's leading entry becomes 1. 將最頂端row乘以某數(純量)使其獲得leading 1.
- Add/subtract multiples of the top row to the other rows so that all other entries in the column containing the top row's leading entry are all zero. 使用ERO中的加法操作使得頂端row的leading1所在column其他全為0
- Repeat steps 2-4 for the next leftmost nonzero entry until all the leading entries are 1. 重複步驟2-4直到得到所有leading1
- Swap the rows so that the leading entry of each nonzero row is to the right of the leading entry of the row above it.交換row位置使得上邊row的leading位置均在下邊row左邊
高斯約旦消去法例子:
試解綫性系統:
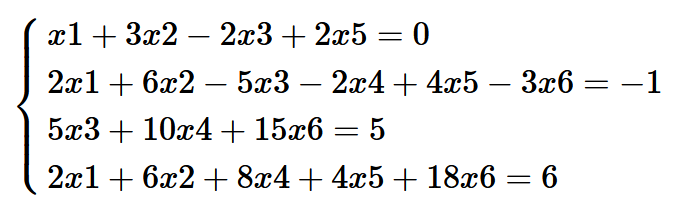
解: 
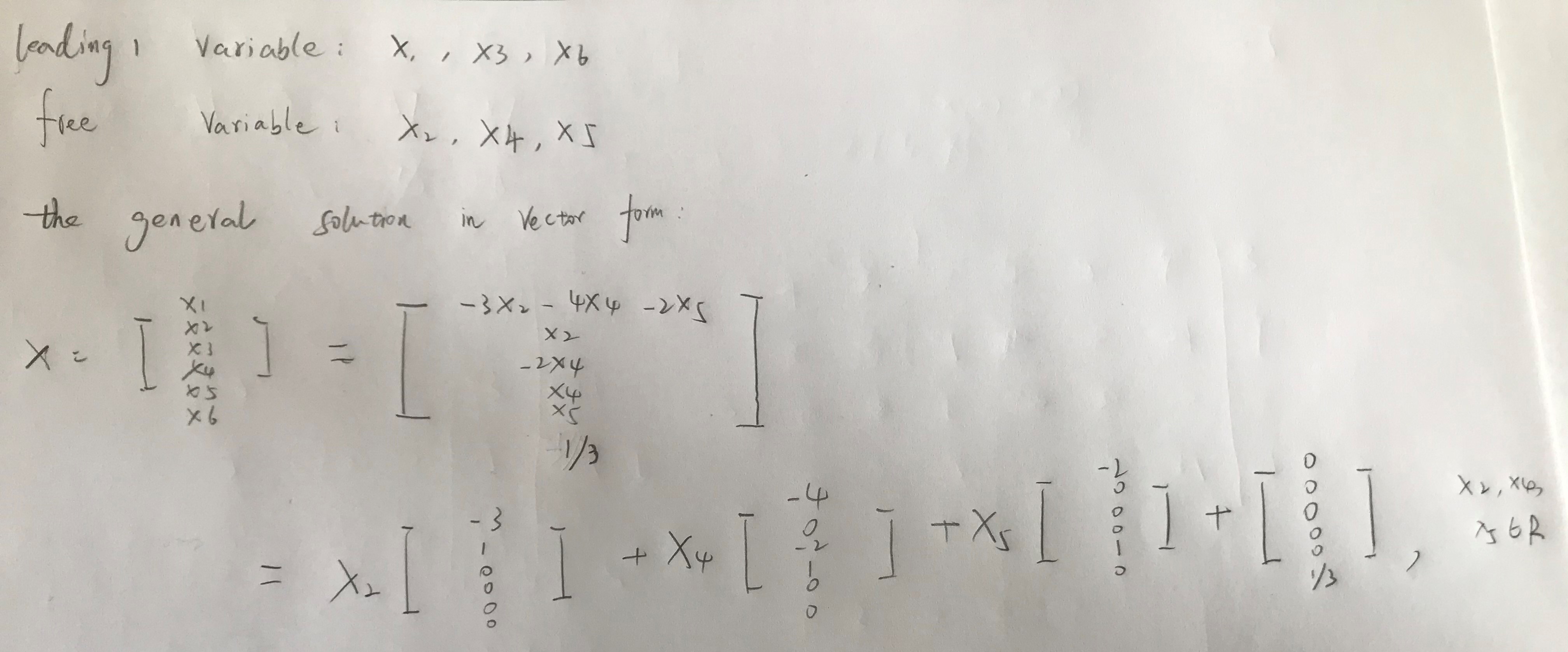
Def of a solution of a linear system: > A solution of a linear system in n knowns x1,x2,...,xn is a sequence of n numbers s1,s2,...,sn such that each equation is satisfied when we substitute x1 = s1, x2 = s2,..., xn = sn.
Def of set of all solutions of a linear system: > The set of all solution of a linear system is called its solution set or the general solution.
Note:
- solution vector

- A linear system is consistent(相容的) if it has at least one solution and inconsistent if it has no solution.
Theorem:
every system of linear equations has either no solutions, exactly one solution, or infinitely many solutions. 線性系統要麽沒解,要麽有唯一解,要麽由無窮多解。
無解情況:
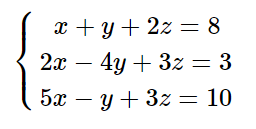
可解得REF:
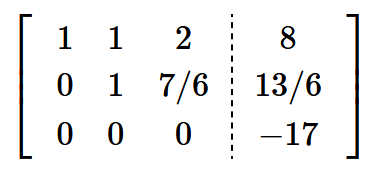
對於最下邊row而言,0=-17顯然衝突,無解。
證明綫性系統不會有大於一個有窮解:
proof:
suppose that the linear system AX=b has finite solutions, say x1,x2 are two distinct solution of AX=b. i.e. A * x1 = b, A * x2 = b then let X = x1 + k(x2-x1),k is a scalar
=> A * X = A * (x1+k(x2-x1)) = Ax1 + k(Ax2-Ax1) = b + k(b-b) = b
i.e. X = x1 + k(x2-x1),k∈R is the solution of the AX=b.It fellows that the linear system AX=b has infinitely many solution.
假設有兩個相異解->有這兩解構造某含參數解->得到結論(兩個相異解會產生無窮多組解)-> 綫性系統不會有大於一個有窮解
Homogeneous(齊次) linear system
形如: AX=0
properties:
- X=0 is the trivial solution of AX=0 and hence AX=0 is consistent
- AX=0 has exactly one solution or infinitely many solution
Theorem: > if a homogeneous linear system has n unknowns, and if the reduced row echelon form of its augmented matrix has r nonzero rows,r<=n,then the linear system has n-r free variables.
proof of this theorem:
The reduced row echelon form of its augmented matrix has r nonzero rows -> it fellows that the homogeneous linear system has r leading1's variable
also number of leading1's variables + number of free variables = n -> number of free variables = n - number of leading 1's variables = n - r
後記
注意: * 某矩陣的RREF最後一row全為0並不能代表該系統一定有無窮多組解。因為原矩陣可能equation數大於unknown數,即原矩陣中可能有冗餘的條件。
參考
- wikipedia
- https://www.statlect.com/matrix-algebra/augmented-matrix
- https://online.stat.psu.edu/statprogram/reviews/matrix-algebra/gauss-jordan-elimination
