前言
機率統計的一開始是複習之前離散數學的排列組合知識,因為我離散數學已經學完兩年忘記了很多,正好也重新整理下,不過這部分肯定沒有宜豊老師教的那麼深入那麼難。 本文的排列P符號和組合C符號和重複組合H符號的符號右邊數字表達上,因為大陸表示法和國際表示法似乎顛倒,而文中均涉及,會意即可。
引題
n根相同天線,假設兩根連續壞掉才會導致系統壞掉。請問若n支天線中恰有m支壞掉,則該系統正常運轉之機率為何?
①m≤1時
顯然此時系統正常,正常運轉機率為1
②m≥2時
考慮壞與不壞的總的情況數為:
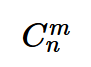
考慮壞掉的情況個數為(連續一組天線位置為損壞的可能性個數 * 剩下位置任選m-2根天線為損壞天線的可能性個數):
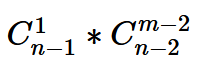
以總情況數為分母,壞掉情況數為分子化簡後得到系統出錯機率為:
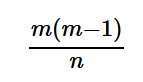
P(系統正常) = 1 - P(系統出錯)為:
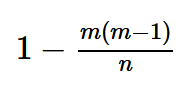
計數的基本原理
假設在r個試驗中,第一個試驗有n1種可能的結果;且對這n1種可能結果的每一結果,第二個試驗都有n2種可能結果;且對前二個試驗的每一個可能結果,第三個試驗都有n3種可能結果;且對...,那麼此r個試驗總共有n1* n2 * n3...*nr種可能結果。
排列(Permutation)
定義: >In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order.
- 全排列:對n個元素進行全部排列稱為全排列,公式為:
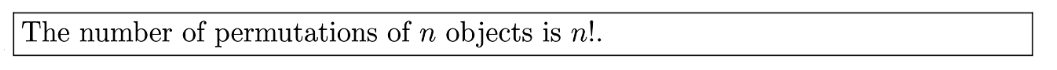
- 部分排列:對n個元素中取m個元素做排列稱為部分排列,公式為:

理解:所有元素全排列後去除重複計數部分(對每一種全排列情況,都重複計數了剩餘元素n-r的全排列次)
- 環狀排列:
對於在一個環來說,只要兩元素之間的相鄰關係不變則視為同一個環,所以要在全排列的基礎上除以元素總個數,化簡後公式為: 
- multisets的排列(有多種相同元素形成之集合的排列): 因為同一集合下元素相同,所以先視為不同元素做全排列後需要除以各集合元素個數的階乘去重。(對於所有元素全排列下,每個集合各自重複了集合元素個數的全排列數)
If the multiplicities of the elements of M (taken in some order) are m1,m2,...,ml and their sum (that is, the size of M) is n, then the number of multiset permutations of M is given by the multinomial coefficient:
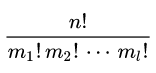
如:
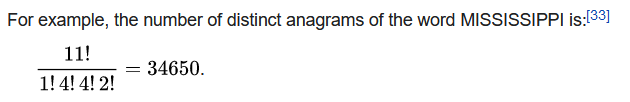
組合
定義: >In mathematics, a combination is a selection of items from a collection, such that the order of selection does not matter (unlike permutations).
對於集合S(其元素個數為n)下,取k個元素可以形成的情況個數為:

理解:所有元素全排列後去除重複計數部分(對每一種全排列情況,都重複計數了r個元素的全排列次*剩餘元素n-r的全排列次)
Pascal's rule : 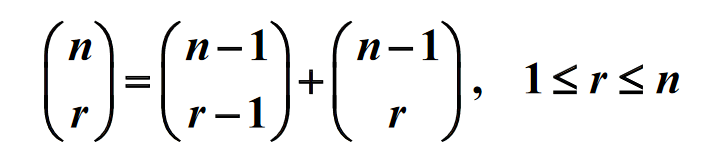
組合總數((x+y)^n係數和):
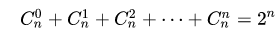
組合總數證明(以二項式公式證明): 
二項式定理
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)^n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b.
公式:
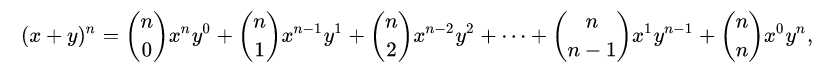
或表達為:
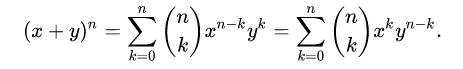
二項式定理證明:
- 數學歸納法:

其中比較tricky的兩個點是:
建立j=k-1的關係,一個是迎合後邊整合,一個是提出b的最高次冪項
運用pascal rule合併兩個組合數 * 組合方法:

這是一種直觀理解轉換為一定數學語言的證明方法(不過怎麼看著不太學術@@)
多項式定理
為了方便定義如下:
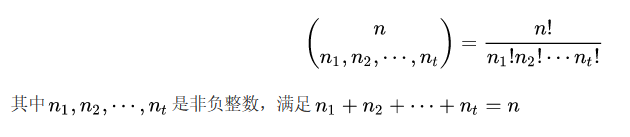
引入多項式定理項數計算:
把 n 个小球放入到 r个有区别的盒子中(盒内无序),使得第一个盒子里边装有 n1 个小球,第二个盒子里边装有 n2 个小球,…,第 r 个盒子里边装有 nr个小球,并且满足 n1+n2+...+nr=n,求不同放法的个数。等價於:將n個資源放入r個不同盒子,可以空,求不同放法個數。
故多項式展開項數為:
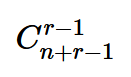
多項式展開合併後每一項前係數為(從n個連乘的(x1+x2+...+xm)中取n1個得到項中x1的冪,從n-n1個中取n2個得到項中x2的冪,以此類推計數,所有的組合的數量即項前係數大小):
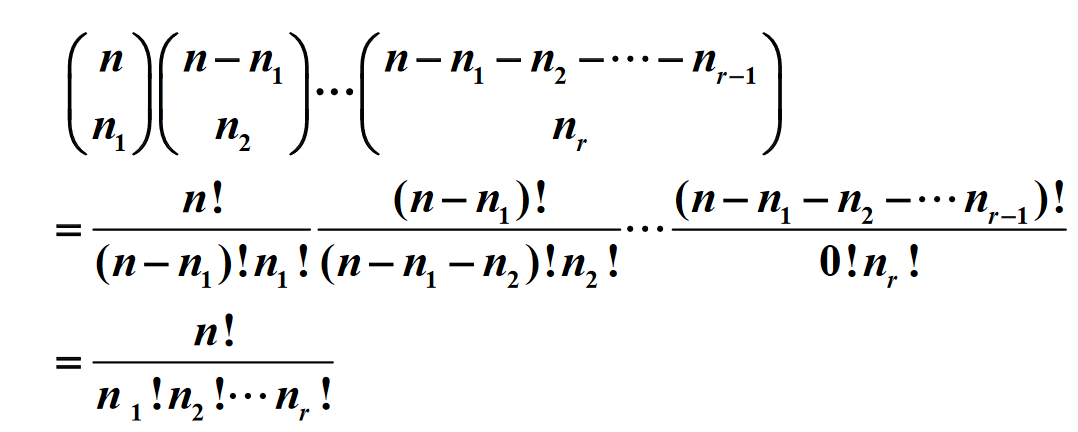
定義:

太久沒碰了,竟然連連乘符號都完了,補充:

組合公式應用:求方程式整數解個數
將n個不同的球分配到r個盒子中,共r^n種可能的結果。 每一個球都可以選擇前往r個盒子中的一個,所以共r^n種可能。不同於多項式係數計算的點在於其球為不同的球,視為不同資源,而多項式定理係數的分配為相同資源。
對於方程:x1 + x2 + .... + xr = n
求其正整數解集數量:可轉化為將n個相同資源分配到r個不同袋子中,而且袋子不可為空,結合隔板插空法,所以即從n-1個空中組合r-1個空作為隔板位置。即:
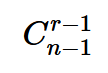
求其非負整數解集數量:可轉化為將n個相同資源分配到r個不同袋子中,而且袋子可以為空,結合隔板插空法,所以即從n+r-1(資源數加上隔板數)個位置中組合r-1個位置作為隔板位置。即:
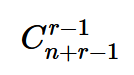
例題1:

可轉化為求方程:x1 + x2 + x3 = 4,x1為取白球個數,x2為取紅球個數,x3為取黑球個數 的非負整數解集個數(將4個取球的機會分到三種可取顏色)。用分隔板法故答案為:
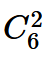
例題2:
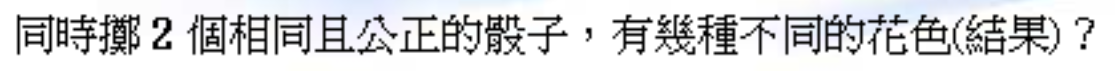
可轉化為求方程:x1 + x2 + x3 + x4 + x5 + x6 = 2 ,x1為擲到1的次數其他同理, 的非負整數解集個數。隔板法結果為:
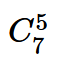
也可以直接考慮為全排列再去除重複計數的部分(除了兩個點數一樣的都被重複計數了一次)
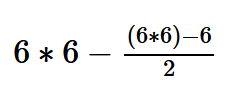
需注意習題集
習題1:

這邊要注意要除以2!,因為組合公式中蘊含了兩不同分類關係,而本題未要求區別分類
參考
- Wikipedia
- 不用数学归纳法,如何证明二项式定理? - 周佳铭的回答 - 知乎 https://www.zhihu.com/question/50613159/answer/134262899
- 百度百科
