前言
因為交換和疫情的緣故,導致我大四下才有機會修線性代數最後一學期沒法混了。現在還沒開始上課,於此先把矩陣運算總結下。
矩陣定義
A matrix is a rectangular array of numbers (or other mathematical objects) for which operations such as addition and multiplication are defined. --Wikipedia
矩陣是長方形的數學式(數字或表達式)陣列,其定義了一些諸如加或乘的操作。
矩陣細部概念
The numbers, symbols, or expressions in the matrix are called its entries or its elements.
矩陣內的數字或表達式叫做矩陣的entry/element
The horizontal and vertical lines of entries in a matrix are called rows and columns, respectively.
豎者叫column,橫者叫row
A matrix with m rows and n columns is called an m × n matrix, or m-by-n matrix, while m and n are called its dimensions.
m個row,n個column的矩陣叫做m×n的矩陣,或者叫做m-by-n的矩陣,其中m與n是矩陣的維度。
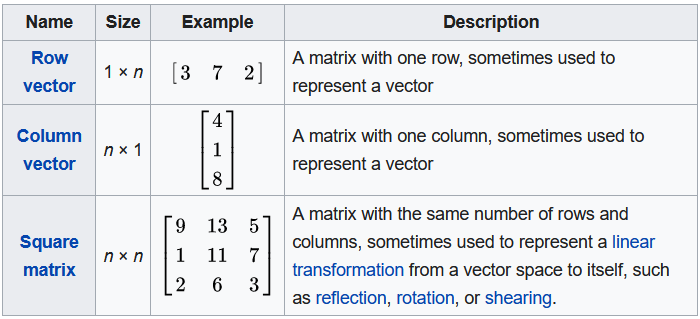
Matrices with a single row are called row vectors, and those with a single column are called column vectors.
只有一個row的矩陣叫row vector。只有一個column的矩陣叫column vector。
A matrix with the same number of rows and columns is called a square matrix. N of rows = N of clomuns的矩陣叫做square matrix(方陣)
row數和column數都相同的兩個矩陣稱為同型矩陣 ## 矩陣表示方法
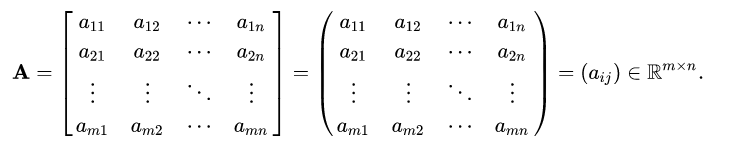
可以用方括號或者圓括號把elements圈起來表示矩陣,或者使用代數式表達(其中R for real number)。
矩陣基本運算
矩陣加法運算

僅適用於同型矩陣,將同型矩陣對應element做加法得到的新矩陣即為矩陣加法運算結果。
矩陣減法運算 僅適用於同型矩陣,與矩陣加法運算類似,僅計算element時改為對應差作為結果矩陣之element。
矩陣數乘運算
The product cA of a number c (also called a scalar(純量) in the parlance of abstract algebra) and a matrix A is computed by multiplying every entry of A by c :(cA)i,j = c · Ai,j.This operation is called scalar multiplication
矩陣數乘運算將矩陣中每一個element乘以常數,得到的矩陣即為數乘運算結果矩陣。 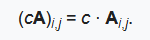
如下例: 
矩陣數乘運算滿足結合律和分配律
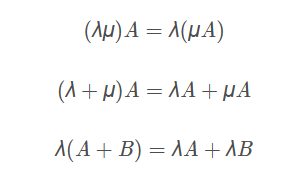
- 矩陣乘法運算
Multiplication of two matrices is defined if and only if the number of columns of the left matrix is the same as the number of rows of the right matrix.
兩個矩陣的乘法運算僅適用於左側矩陣的column數等於右側矩陣的row數時。
If A is an m-by-n matrix and B is an n-by-p matrix, then their matrix product AB is the m-by-p
乘法運算得到的新矩陣其row數等於左側矩陣row數,其column數等於右側矩陣column數。
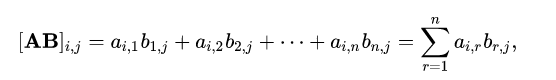
每一乘法結果矩陣element值滿足上圖公式。
矩陣乘法不一定滿足交換律,滿足結合律和分配率, 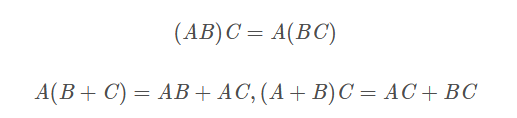
矩陣乘法一般不可兩端消去: 
例如:
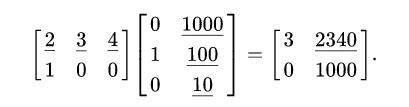
lemma:
If A is an mXn matrix and B is an nXr matrix, then
<A> jth column vector of (A·B) = A · [jth column vector of B]
<B> ith row vector of (A·B) = [ith row vector of A] · B
proof of <A>:
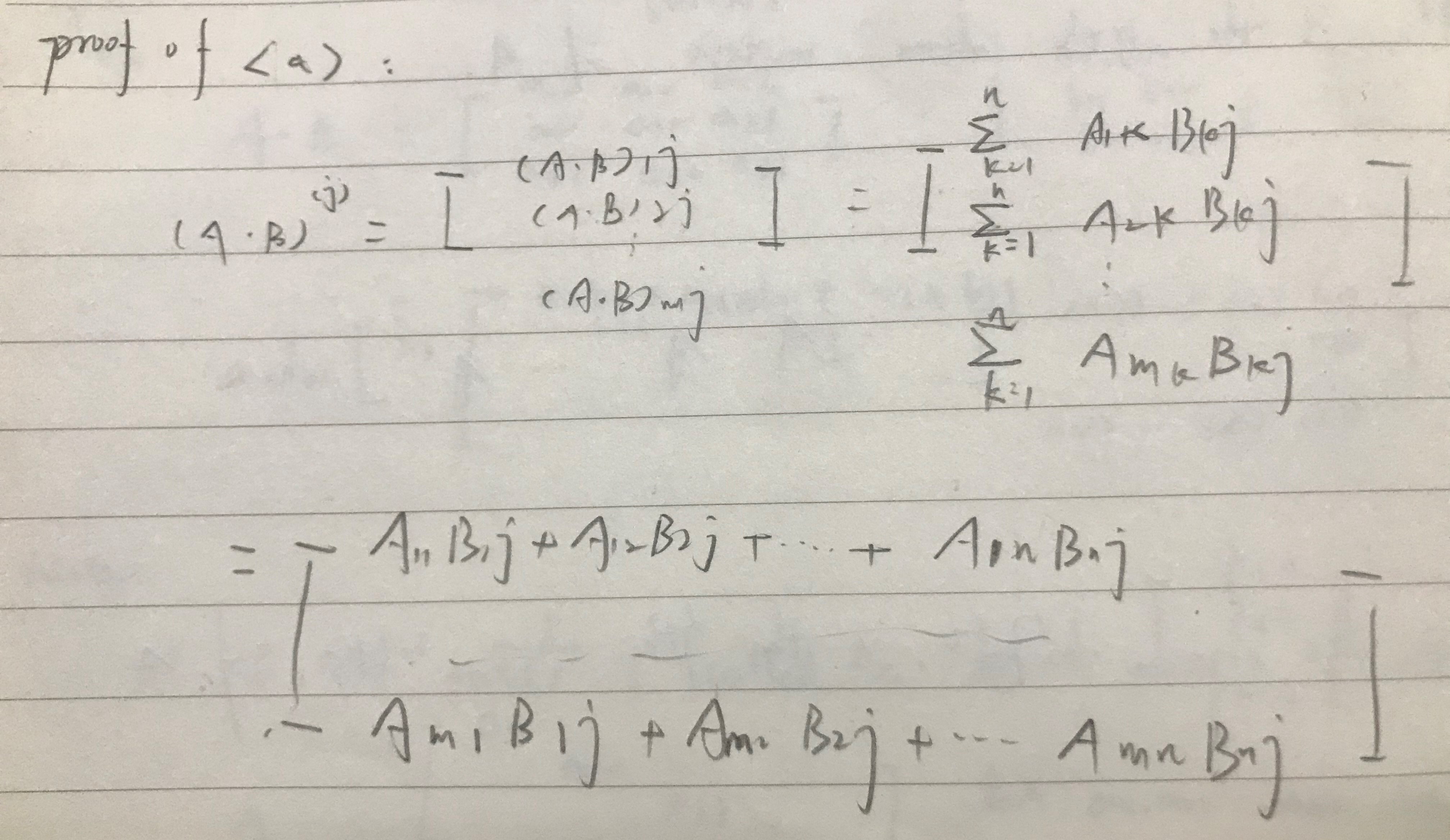
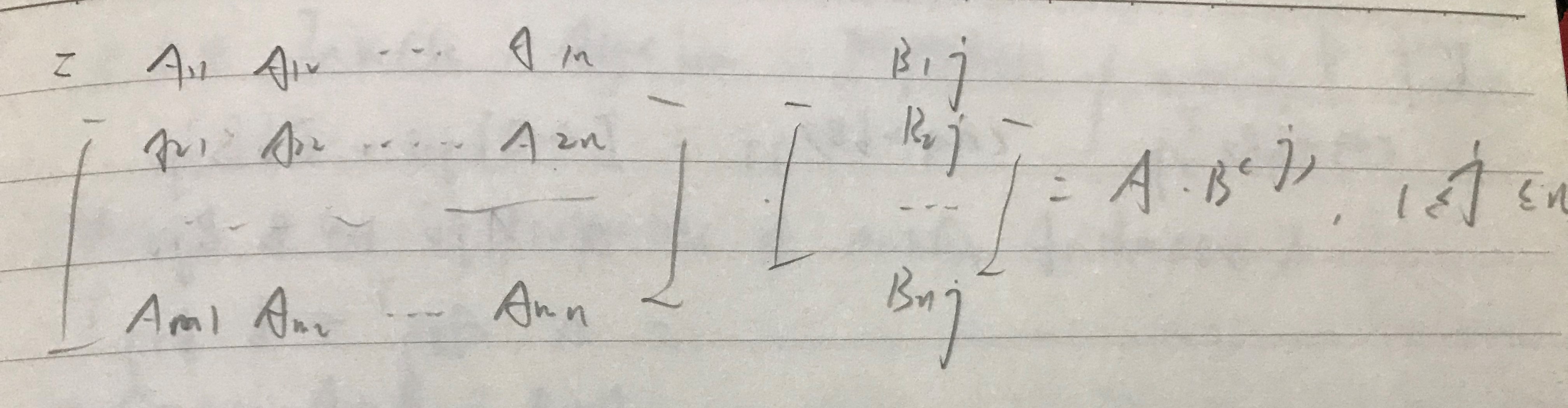
證明思路:回歸矩陣乘法的定義,將(A·B)的jth column拆成累加式,後提出累加式中B的jth column得證。
- 矩陣冪運算
矩陣冪運算僅適用於方陣,連乘冪次即可。(因為矩陣乘法僅適用於左陣column等於右陣row時,又冪運算需自身連乘,所以只有方陣滿足)
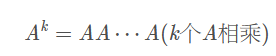
且矩陣的0次冪結果為該矩陣的單位矩陣(對角線為1且其餘皆為0,與原矩陣等大的矩陣) > identity matrix: In linear algebra, the identity matrix (sometimes ambiguously called a unit matrix) of size n is the n × n square matrix with ones on the main diagonal and zeros elsewhere.

滿足:
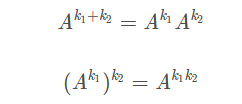
注意不一定滿足: 
因為展開後對比左右要注意到矩陣乘法不一定滿足交換律,即:
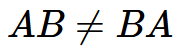
- 矩陣轉置操作
The transpose of an m-by-n matrix A is the n-by-m matrix AT (also denoted Atr or tA) formed by turning rows into columns and vice versa:(AT)i,j = Aj,i.
矩陣轉置即將矩陣的row與column互換
如下例:
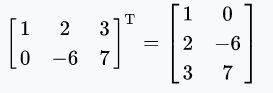
滿足:
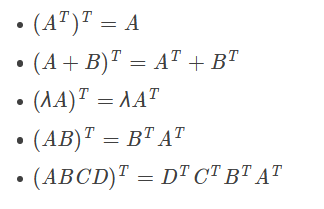
Proof:
式一:
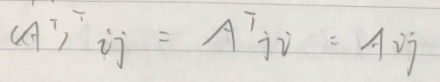
式四: 
式二: 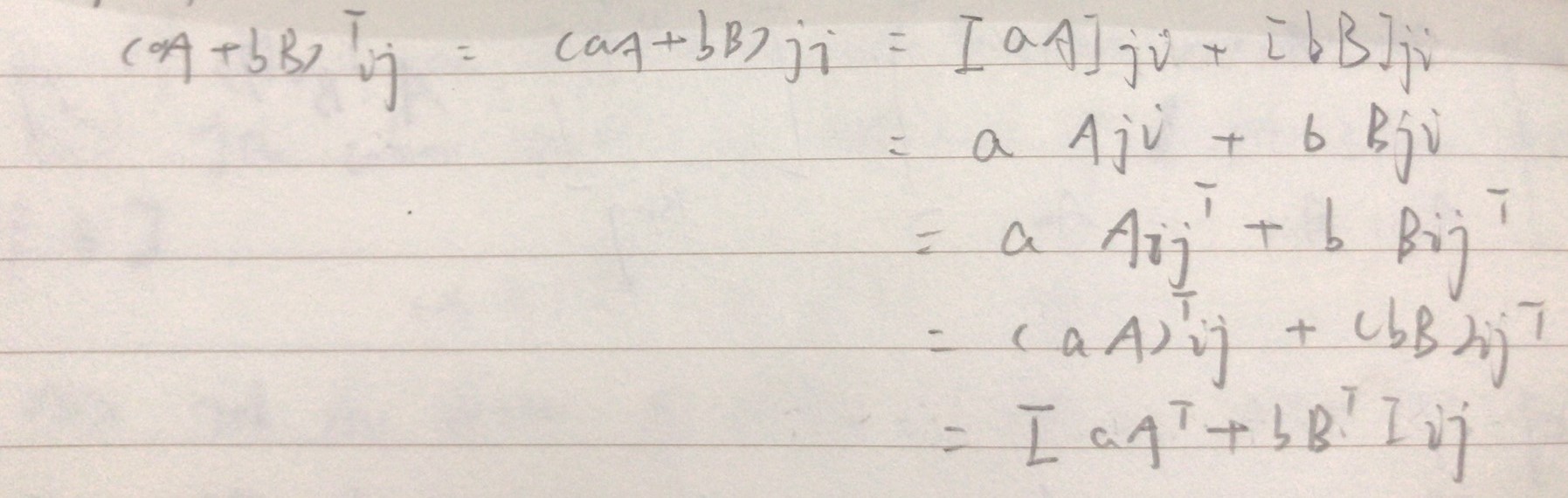
把握住關鍵代換(matrix)^T ij = (matrix)ji
方陣之tr
if A is a square matrix, then the trace of A, denoted tr(A) is defined to be the sum of the entries in the main diagonal(主軸) of A.
i.e. tr(A) = sum of akk (1<=k<=n) ## 後記 因為臨近考試在複習,所以為了節省時間一些證明直接對筆記拍照上傳,可能會比較潦草,之後有空會用LaTeX做的漂亮些。
參考
https://en.wikipedia.org/wiki/Matrix_(mathematics)
https://blog.csdn.net/linxilinxilinxi/article/details/91529083?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.control&dist_request_id=fcba8008-005d-4d69-b8b0-023c9bc78b3b&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.control
